Voici l'énoncé:

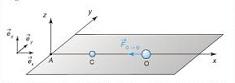
Le ref du labo est galiléen Rg(A,ex,ey,ez) et l'effet de pesanteur est négligeable
Une molécule diatomiq CO est cnstituée d'un atome C de masse mc et d'un atome O de masse mo

Les atomes snt assimilés à des pts matériels et snt repérés par leur abscisse rspective xc et xo.
Leur mvt a lieu selon l'axe (A,ex) et est limité à la demi droite [Ax)

La force qu'exerce C sur O est F(CO)=( -B₁/x⁷  +  B₂/x¹³)ex

Les cstes B₁ et B₂ snt positives et x= xo - xc est la distnce relative entre les 2 atomes. Les 2 éléments ne snt soumis qu'à la force dintéraction d'origine électromagnétique.
L'étude sera effectuée dans le ref barycentrique R* associé au centre de masse G du système des deux atomes.

Bonjour!

J'ai hâte de connaître la question ... x(t) peut être?

1/Justifier le caractère galiléen du ref barycentrique
2/Ecrire les 2 équations differentielles du mvt de C et O dans le ref barycentrique R*. En déduire l'équation du mvt du mobile réduit M dnt vous préciserez les caractéristiq.
3/Déterminer l'énergie potentielle d'interaction Ep(x) de la molécule. L'origine de cette énergie est choisie pour une distance infinie séparant les 2 atomes.

Tout d'abord je voudrais d'abord réussir à répondre à ces questions après jverrai les autres ^^ .

J'ai déjà répondu à la question 1) mais je ne sais pas si ma réponse est bonne.

Puis après je ne sais pas trop.

La réponse 1) est bonne ?

Bonjour

Merci pour l'énoncé

Concernant ta réponse à la question 1) je pense que tu as compris mais je ne suis pas sûr que ta formulation soit très heureuse:

1) le référentiel R (du labo) l'est par définition
2) le système {C;O} est isolé, la pesanteur étant négligeable

Donc, le référentiel barycentrique de ce système est aussi galiléen

Le principe d'intertie y est DONC vérifié et les lois de Newton s'y appliquent.

Est ce plus clair?

Ensuite tu fais le bilan des forces sur C et O et en appliquant les 2eme et 3eme lois de Newton, tu arrives (normalement) aux equations différentielles demandées.

N'hésite pas si tu as besoin de précisions/vérifications ultérieurement

Il y a que F(CO) qui est exercé ?

donc ma = F(CO)

Re,

On avance. C'est bien ...

La force étant le long de l'axe Ox, c'est donc d²x/dt² qui va nous intéresser.

Comme la résultante des forces est la somme de:
- une force d'attraction (Van der Walls) en 1/x⁷
- un force de répulsion (recouvrement) en 1/x¹³
qui auront des intensités sensiblement différentes selon la valeur de x, tu peux déjà prévoir un mouvement d'oscillation ... qu'il te reste je pense à décrire quantitativement. Courage!

Donc m (d²x/dt²)= F

(jcomprends pas vraiment comment avoir les equations diff ici ^^' )

Hum, hum,  

On y est pourtant presque ...
Je te propose d'indexer * les coordonnées dans le référentiel R*

On a donc:






Ecrivons dans R* la 2nde loi de Newton pour O:



C'est parti?

ok att

donc pour C c'est l'inverse, hein ?

mc. d²xc*/dt²= + B1/x⁷  -  B2/x¹³   ?

(mo.a=F

mc.a= - F) ?

tout à fait!

Après je ne sais pas comment répondre à la question 2

Bonjour,

La combinaison des 2 équations différentielles issues de la 2nde loi de Newton te donne



L'énoncé te "guide" en te proposant d'utiliser le mobile réduit M, dont les caractéristiques (cf. cours peut être) sont:



et de masse

ce mobile fictif étant soumis à la force

Tu résous l'équation différentielle ci dessus (tu te rappelles qu'une primitive de est )

En suite, considérant que la force est conservative (elle ne dépend que de la distance entre les 2 atomes) et que l'E_p du mobile réduite est l'énergie potentielle d'interaction entre O et C:

, tu intègres avec d'après l'énoncé E_p=0 à l'infini

Est ce plus clair ainsi?

moi je trouve ça:

Ep(O)= - B1/6x^6   +   B2/12x^12

Ep(C) = +B1/6x^6   -   B2/12x^12

car Ep(O) = - Int( - B1/x^7   +   B2/x^13 ) dx

OK ... sauf que ta formulation se semble (un peu) maladroite

L'énergie potentielle est celle de la molécule, donc celle de la particule fictive M soumise à .

Formulé différemment: c'est l'interaction entre les deux atomes qui est la source de ce potentiel. Il ne faut donc considérer qu'un seul des atomes (n'importe lequel d'ailleurs) pour comptabiliser l'énergie potentielle (cf. analogie pesanteur)

donc pour bien rédiger la question 2/ et 3/ je fais comment ??

(je sais pas comment jdois rediger ces réponses...)

Bonjour,

Une fois que tu as défini la particule réduite M, de coordonnée x dans R*, tu confonds ta molécule et le point M (tu peux le faire dans le ref barycentrique) et donc tu ne parle plus que de x et de M, l'énoncé d'ailleurs te demande Ep(x) de la molécule, donc du mobile M.

Est ce plus clair ainsi?

oui ^^ et pour cette question : " En déduire l'équation du mvt du mobile réduit M dnt vous préciserez les caractéristiq." j'dis quoi ?

ah non g rien dit ^^

Post du 2 mai à 12:21