bonjour

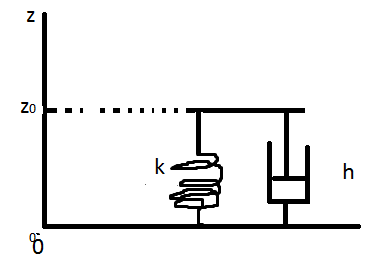
On considère un système d'amortissement posé au sol recouvert d'un plateau de masse m=100kg. ce système est constitué d'n ressort de raideur k=5*10^5 N.m^(-1) couplé a un amortisseur de coefficient b= 5*10^4 Kg.s^-1.
L'amortisseur et le ressort exercent respectivement, sur le plateau  une force  de rappel  Fk= -k(z-lo), où lo est la longueur à vide et un e force de frottement visqueux Ff=-bv.
Soient(O,ez) l'axe vertical ascendant et g la norme de la pesenteur

1) En écrivant la lois fondamentale de la dynamique appliquée au plateau et en projetant cette lois suivant l'axe vertical Oz, déterminer l'équation de son mouvement en fonction de z

réponse: ext= ma = Fk + Ff + mg (vecteur)

ma = -k(z-lo)- bv +mg

m d²z/dt = -k(z-lo) - b dz/dt +mg

m d²z/dt² + b dz/dt + k(z-lo) -mg =0

je sais pas si c'est cela qu'il faut trouver

2)Soit le changement de variable: Z(t)=z(t)-zo. Montrer que l'équation du mouvement devient

d²Z/dt² +(2/C)*(dZ/dt) +w²Z=0
Où vous déterminerait  c et w en fonction des données du problème en donnant leur  dimension physique.
quelle est la solution mathématique de la solution Z de cette équation

réponse: je sais pas comment trouvé peut être que je me suis trompé en haut



Edit Coll : image recadrée