Inscription / Connexion Nouveau Sujet
superficie d'une tranche d'une sphère
Bonne soirée
Voila je bloque juste au début d'un exercice d'électrostatique,
L'énoncé:
Potentiel créé par une sphère conductrice de centre O,de rayon R,portant une charge Q uniformément répartie à sa surface en un point M tel que OM > R
Pour cela,on doit considérer une surface dS du sphère représentée par une tranche(le shéma attaché(vite fait
).
A' mon avis la surface de la sphère délimitée par la tranche peut etre considérée comme un rectangle de langueur 2
.PH et de largeur dx,soit: dS = 2.PH.dx or dans le corrigé j'ai trouvé :
dS = 2.PH.dx/sin
est-ce quelqu'un peut m'expliquer cette formule??.
Je vous remercie
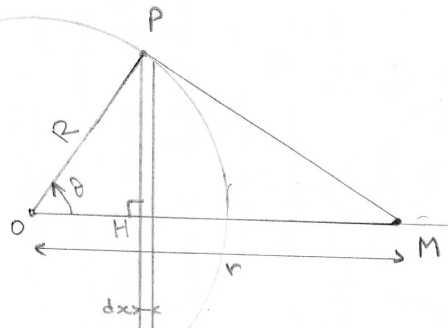
L'élément de surface dS est égal à 2.PH.ds, ds étant la petite partie du segment PM, tangent à la sphère en P, découpée par la tranche d'épaisseur dx. Or on a dx = ds sin.
merci beaucoup Priam
C'etait exactement ce que je viens de trouver sur mon cahier,mais ça reste étrange de dire que la largeur de notre rectangle n'est pas dx mais PF(comme je l'ai nommé dans le nouveau shèma).
Donc: dS = 2.PH.PF
or cos(/2-) = sin = dx/PF
PF = dx/sin
dS = 2.PH.dx/sin
mais cela reste toujours étrange hhhh
mercii
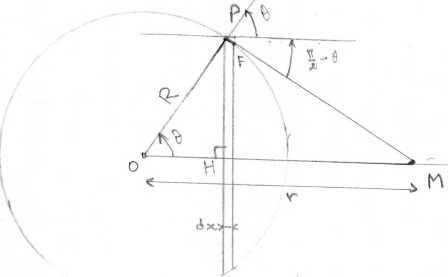
Il ne faut pas ici considérer un rectangle.
Considère plutôt que la surface latérale de la tranche de sphère d'épaisseur dx est assimilable à celle du tronc de cône de hauteur dx, laquelle est engendrée par la rotation de l'élément PF (orienté obliquement) autour de l'axe OM à une distance PH.
Annuler
connectez vous