Inscription / Connexion Nouveau Sujet
Stokes
ameliz
Bonjour j'ai une question sur cette exercice :
Dans cet exercice nous vérifions le théorème de Stokes pour :
et le quart de disque S (rayon 1, centrer à l'origine, dans le plan yz) : la figure ait en dessous.
(a) Calculer , trouver un paramétrage de S et son vecteur normal unitaire
. Donner :
(b) Orienter la frontière C de S, exprimer chacun des trois morceaux avec un paramétrage. Calculer :
Alors en fait j'en suis que au tout début de la a :
rot A = - i - j - k (A, i j et k étant des vecteurs)
Ensuite, il faut trouver un paramétrage de S.
Je dirais qu'on paramètre ce quart de cercle par : x=cos(t) et y=sin(t), avec t décrivant [0;pi/2].
Est-ce que c est correct ce que j'ai fait jusqua présent ?
Que faire pour la suite ?
je reposte ici car c'est pluis de la physique que des maths en fête
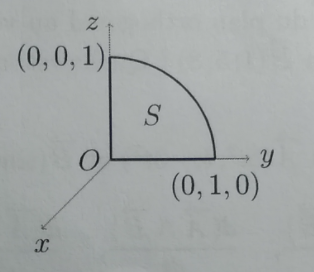
Bonjour
L'idée d'un paramétrage en utilisant les coordonnées polaire est très bonne : variable 
plutôt que t peut-être. Ensuite comment écrire en polaire un déplacement élémentaire sur cet arc ?
Bonjour,
Vous confondez quart de cercle à paramétrer comme vous le dites (cela c'est pour le b) et quart de disque S, pour lequel on peut se dispenser de paramétrage (cela c'est pour le a). Si vous tenez à paramétrer S, S est une surface donc il faut deux paramètres. Pour le a, il manque la détermination du vecteur normal.
Il faut calculer le flux du rotationnel d'une part, et la circulation de A d'autre part.
Vous devriez trouver la même chose.
merci de ses réponses
quelle est la différence entre le quart de cercle S et le quart de disque S ?
a la question a il s'agit de quoi ?
Attention à tes notations : bien faire la différence entre un déplacement élémentaire le long du contour fermé qui peut se noter et un élément de surface orientée qui peut se noter
.
Le paramétrage en polaire est pertinent pour déterminer la circulation du vecteur le long de l'arc de cercle.
Concernant le flux du rotationnel à travers le quart de disque, autant, me semble-t-il, rester en coordonnées cartésiennes.
D'accord avec ton expression du rotationnel.
Un cercle est une courbe le long de laquelle on calcule la circulation d'un vecteur. Un disque est une surface à travers laquelle on calcule le flux d'un autre vecteur : le rotationnel de l'autre vecteur...
Rem : même ordre d'idée : bien faire la différence entre une sphère (surface) et une boule (volume délimité par la sphère).
merci de ces clarifications. J'en ai bien bezoin car je viens d'intégrer une école d'ingé mais avant j'étais en iut dans un total autre domaine donc tout ça je ne l'ai jamais vu alors c'est très dur pour moi
donc je résume pour la question a :
puis paramétrage du quart de disque S :
x=cos() et y=sin(), avec décrivant [0;
/2].
Est correct jusqua présent ? Quoi faire pour la suite ?
Tout va bien pour l'instant. Tu commences par étudier la circulation du vecteur le long du contour fermé.
Dans la base polaire , un vecteur déplacement élémentaire le long de l'arc de cercle peut s'écrire :
La circulation doit aussi être calculée le long des segments en gras sur la figure pour avoir un contour fermé.
oki merci mais maintenant comment calculer ? Je sais pas calculer les doubles intégrales....
et pq ils demandent de paramétrer le vecteur unitaire n ? il serre à quoi ?
Bonsoir,
@ameliz : le multi-post est strictement interdit sur le forum 
:
la FAQ du forum
) :
Tu as en effet déjà demandé de l'aide côté maths, tu continues donc là-bas :
Annuler
connectez vous