Inscription / Connexion Nouveau Sujet
Statique : Indiana Jones
Bonjours, j'ai besoin d'un peu d'aide sur certains points.
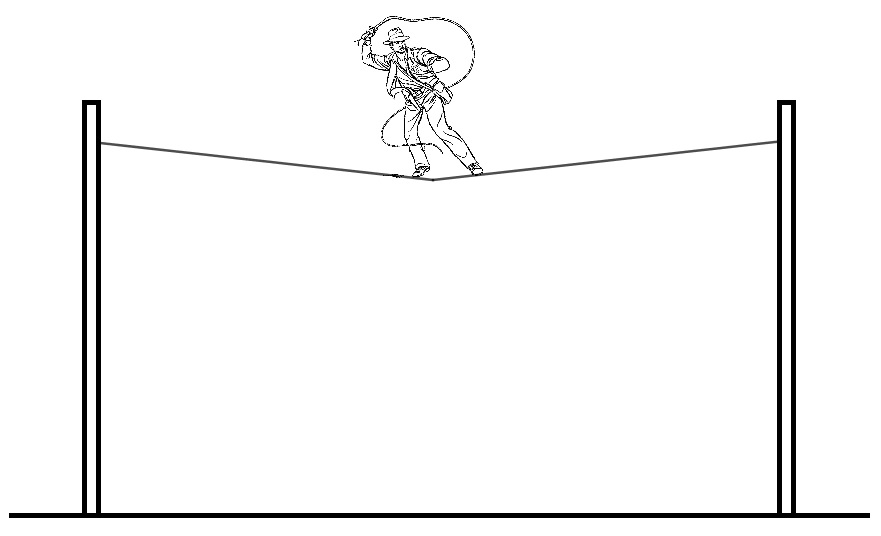
Lors de ses péripeties, Indiana Jones se retrouve au milieu d'un point de lianes. Pour s'implifier on considérera le pont comme une corde attachée a deux poteaux fixes et Indiana Jones sera considéré comme une masse ponctuelle 70 kg placée au milieu de la corde.
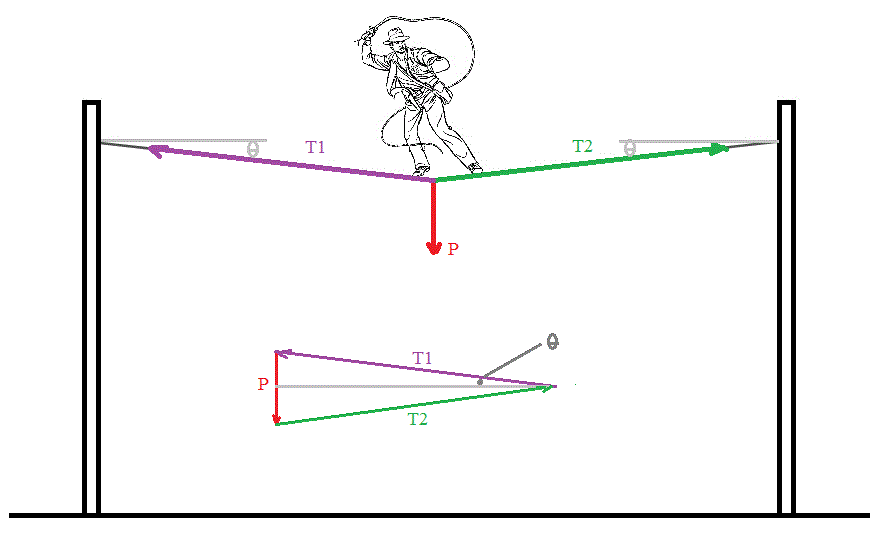
J'ai réussi a faire le schéma avec les forces appliqués
J'ai réussi à écrire les forces composantes
Je n'arrive pas à prouver que T1 et T2 ont la même norme (je sais qu'on doit utiliser le principe fondamental de la statique).
ET je dois également déterminer la tension T de chacun des deux brins pour maintenir l'équilibre.
Hello
La liane a t elle une masse? On bien la négliges tu?
Peux tu préciser quel est le système (l'objet) auquel tu vas appliquer le relation fondamentale de la statique et recenser les forces qui lui sont appliquées?
Bonjour
Il faut commencer par remarquer que, dans un triangle isocèle, deux des trois angles internes sont égaux. Cela va te permettre de montrer que les deux vecteurs T1 et T2 ont la même inclinaison par rapport à l'horizontale. Ensuite, Il suffit d'écrire que la masse est en équilibre sous l'action de trois forces. En projetant sur un axe horizontale la relation vectorielle correspondant au principe fondamental de la statique, tu va montrer T1=T2 en norme. En projetant sur un axe vertical, tu vas obtenir cette norme en fonction du poids et de l'angle...
Alors la liane n'a pas de masse. J'applique les forces à Indiana jJones et les forces sont donc sont poids ET T1 et T2 (les lianes).
Merci
Super!
Alors il n'y plus qu'à faire ce que Vanoise (que je salue bien) t'indique plus haut: écrire l'égalité vectorielle traduisant l'équilibre et projeter sur les axes (horizontal et vertical)
Justement j'ai bien compris qu'il faut faire cela, mais je n'y arrive pas; Pourriez vous me montrer seulement le début.
Bonjour à tous,
Vous avez déjà dit ce que j'avais l'intention de poster.
Je me contente donc d'une illustration.

Bonjours, j'ai besoin d'un peu d'aide sur certains points.
Lors de ses péripeties, Indiana Jones se retrouve au milieu d'un point de lianes. Pour s'implifier on considérera le pont comme une corde attachée a deux poteaux fixes et Indiana Jones sera considéré comme une masse ponctuelle 70 kg placée au milieu de la corde.
J'ai réussi a faire le schéma avec les forces appliqués
J'ai réussi à écrire les forces composantes
Px=0 T2x=-T2*cos(o) T1x=t1cos(0)
Py=-mg T2y= T2*sin(o) T1y=T1sin(o)
prouver que T1 et T2 ont la même norme T1cos(o)-T2*cos(o)=0
COs(o)=Cos(o) donc T1-T2=0 Donc T1=T2
ET je dois déterminer la tension T de chacun des deux brins pour maintenir l'équilibre en fpnction de la masse et de l'angle téta. Mais je n'y arrive pas
*** message déplacé ***
JE trouve que T=(2mg)/sin(o)
Pourtant l'exercice demande en fonction de la masse et l'angle mais j'ai aussi g.
Que faire ?
Merci
JE trouve que T=(2mg)/sin(o)
Ton facteur " 2 " est mal placé.
Pourtant l'exercice demande en fonction de la masse et l'angle mais j'ai aussi g.
Que faire ?
Se rendre compte qu'une force (dimension MLT-2) ne peut pas s'exprimer uniquement à l'aide d'une masse et d'un angle
Merci
Pourtant il me semble bien placé, pouvez vous me montrez le début du calcul (pas en entier, pour que je puisse faire la suite tout seul)
Merci
Si  est l'angle entre la direction de la corde et l'horizontale, la projection de la condition d'équilibre sur l'axe Oy donne :
est l'angle entre la direction de la corde et l'horizontale, la projection de la condition d'équilibre sur l'axe Oy donne :
T1 . sin( ) + T2.sin(
) + T2.sin( ) - mg = 0
) - mg = 0
Et T1 = T2 = T
Comme je te l'ai déjà dit :
T qui est une force NE PEUT PAS s'exprimer uniquement à partir d'une masse et d'un angle.
La relation T = mg/(2.sin( )) est exacte.
)) est exacte.
Il est probable que si " g " n'est pas réclamé par l'énoncé, c'est soit un oubli, soit que c'est considéré comme une évidence.
ok, cest logique merci.
Ensuite on me demande de dire sa limite en 0,je trouve +'linfini
C'est le bon résultat,mais c'est incohérant ? non ?




 ) :
) :