Inscription / Connexion Nouveau Sujet
statique du solide
bonjour tout le monde
pourriez-vous svp me corriger la 1ere et la 2 eme réponse ?..par contre je suis bloquée sur la 3eme question si vous pouvez m'aider svp.
je vous remercie par avance.
Une masse m est suspendue à l'extrémité de deux fils inextensibles AC et BC. Le fil AC
est relié au point fixe A . Le fil BC passe sur la poulie B et supporte une masse M . La
distance horizontale entre A et B est L et la distance verticale entre A et B est h.
La position du point C est définie par l'angle α entre CB et l'horizontale. On appelle Tca la tension du fil AC et β l'angle entre CA et l'horizontale.
1. Exprimer les longueurs AC et BC en fonction de L , h , α et β .
2 Exprimer la relation vectorielle qui traduit l'équilibre du système.
3 -En projetant cette relation sur l'horizontale et sur la verticale, en déduire les valeurs de Tca et de β en fonction de m, M et α.
4. Déterminer les valeurs numériques de Tca , β , AC et BC sachant que : l = 1.2m ; h= 0.3 m, m=8kg, M= 5kg , α=38°, g= 10 m.s-²
1. Exprimer les longueurs AC et BC en fonction de L , h , α et β .
On pose :
x = BC et y = AC
y cosβ + x cosα = l
y sinβ - x sinα = h
On aura donc un système de deux équations à deux inconnues x et y à résoudre, et en utilisant les formules d'addition :
y cos β sinβ + x cosα sinβ= l sinβ
y sinβ cos β - x sinα cos β = h cos β
x(cosα sinβ + sinα cos β ) = l sinβ - h cos β
D'où
x= l sin β-h cos β / cosα sinβ+ sinα cosβ
y (cos α sinβ + sin α cos β) = l sin α+ h cos α
y= (l sin α+ h cos α)/(cos α sinβ + sin α cos β)
x= l sin β-h cos β / (sin( α+ β))
y= (l sin α+ h cos α)/ ( sin(α+β) )
BC= l sin β-h cos β / (sin( α+ β))
AC= (l sin α+ h cos α) / ( sin(α+β) )
2 Exprimer la relation vectorielle qui traduit l'équilibre du système.
Nous avons le solide ‘m' en état d'équilibre , c'est-à-dire que la force de son poids P et la force de la Tension T du 2 fils AC et BC ont même droite d'action , même valeur, mais des sens opposés :
P + TAC + TBC = 0
La somme vectorielle des forces vaut vecteur nul, noté
La somme des projections en horizontale et en verticale vaudra 0
∑_(Fx = 0)
TAC - TBC = 0
TAC cos(α) - TBC cos(β) = 0
∑_(Fy = 0)
TAC sin(α) + TBC sin(β) - (m*g) = 0
3 - En projetant cette relation sur l'horizontale et sur la verticale, en déduire les valeurs de TCA et de β en fonction de m, M et α.
TCA cos(α) - TBC cos(β) = 0
donc
TCA = (T BC cos(β) ) / (cos(α) )
TAC sin(α) + TBC sin(β) +(M*g) - (m*g) = 0
TAC sin(α) + TBC sin(β) +(M*g) = (m*g)
(T BC cos(β) )/(cos(α) ) + TBC sin(β) + (M*g) = m*g
Bonjour
Te serais-t-il possible de poster ici un scan de ton schéma avec ci-possible la représentation des vecteurs forces que tu as utilisée pour ton raisonnement ? Il sera ainsi plus facile de vérifier ton travail et de t'aider pour la fin.
bonjour vanoise,
d'abord je vous remercie pour votre aide...
vous trouvez ci-joint le schéma correspondant à l'énoncé .
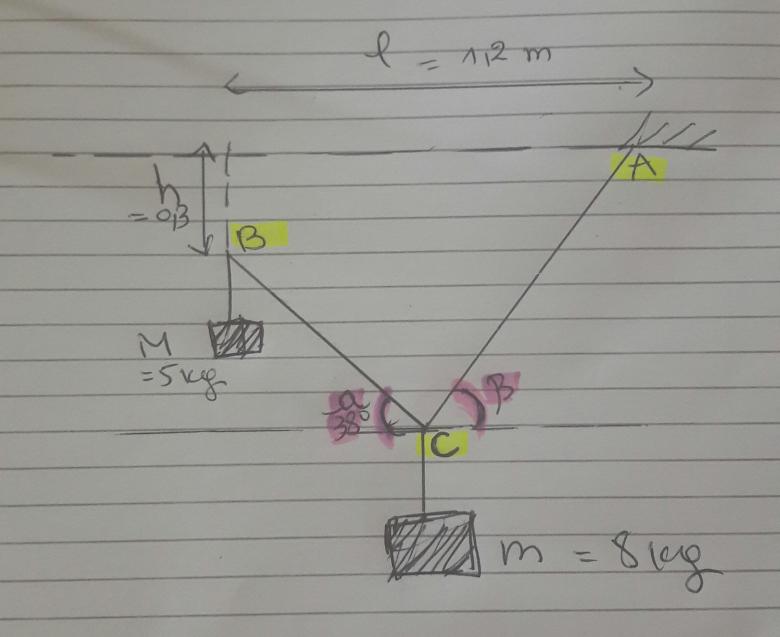
Tout ce que tu as fait est correct sauf les trois dernières lignes. Tu ne prends pas correctement en compte le rôle de la poulie. En supposant celle-ci mobile en rotation sans frottement et en supposant le fil reliant C à la masse M de masse négligeable devant M, on peut considérer que la poulie conserve la tension du fil : le fil exerce la même force (en norme) à chacune de ses deux extrémités donc :
TBC=M.g
La situation devient alors beaucoup plus simple !
Remarque : ce que je viens d'écrire peut se démontrer rigoureusement en appliquant le théorème du moment statique à la poulie et en considérant l'équilibre du fil de masse négligeable mais en général, quand la démonstration n'est pas explicitement demandée, on peut admettre le résultat sur la conservation de la tension du fil le long de celui-ci...
Ce qui veut dire que je dois supprimer Mg
donc j'aurai
TAC sin(α) + TBC sin(β) - (m*g) = 0
TAC sin(α) + TBC sin(β) = (m*g)
TBC=M.g = 50 N
m.g= 80 N
TAC sin(38) + 50 sin(β) = 80 N
mais comment on peut déduire la valeur de β?
Je crois que tu as aussi commis une permutation des deux angles dans certaines formules. Je reprends la projection sur les deux axes de la relation d'équilibre.
Donc :
Donc :
Division membre à membre de (2) par (1) :
Je te laisse terminer...
bonjour vanoise
d'abord je tiens à vous remercier pour vos conseils et vos explications.
voici le complément de réponse si vous pouvez vérifier svp.
3 - En projetant cette relation sur l'horizontale et sur la verticale, en déduire les valeurs de TCA et de β en fonction de m, M et α.
TAC. cos(β) - TBC . cos(α)= 0
TCA = (T BC cos(α) )/(cos(β) )
TAC. cos(β) = TBC . cos(α)
TBC = M .g
Donc :
TAC. cos(β) = M.g . cos(α)
TAC sin(β) + TBC sin(α) = m*g
Donc :
Division membre à membre de (2) par (1) :
4. Déterminer les valeurs numériques de Tca , β , AC et BC sachant que : l = 1.2m ; h= 0.3 m, m=8kg, M= 5kg , α=38°, g= 10 m.s-²
Tan(β) = (m-M.sin(α) )/(M.cos(α) )
Tan(β) = (80-50.sin(38) )/(50.cos(38) )= 1.25
Donc
β= 57°
TCA = (T BC cos(α) )/(cos(β) )
Avec
TBC = M .g= 50 N
TCA = (50 cos(38) )/(cos(57) )= 72.96 N
AC= (l sin α+ h cos α)/( sin(α+β) )
AC= (1.2 sin 38+0.3 cos 38)/( sin(38+57) )
AC= 0.97 m
BC= l sin β-h cos β/(sin(α+ β))
BC= 1.2 sin 57-0.3 cos 57/(sin( 38+ 57))
BC= 0.84m
Je viens de vérifier tes calculs. J'obtiens comme toi tan( =1,25 mais cela correspond à un angle
=1,25 mais cela correspond à un angle  =51,3°
=51,3°
Cela impacte légèrement la suite des applications numériques...


