Bonjour, je suis entrain de faire un exercice sur la statique des fluide. Voici l'énoncé, et je vous met le schéma en pièce jointe :

Exercice 1 : Stone balancing

Une discipline fascinante, et pour le moins intrigante. Le "stone balancing" consiste à construire des œuvres en empilant des pierres dans des dispositions improbables, ne tenant que par un équilibre précaire.
Mais comment cela est-il possible ? C'est que l'on va vous demander de calculer dans cet exercice. Bien sûr, nous allons pour cela simplifier la géométrie des pierres présentes sur la photo ci-contre.

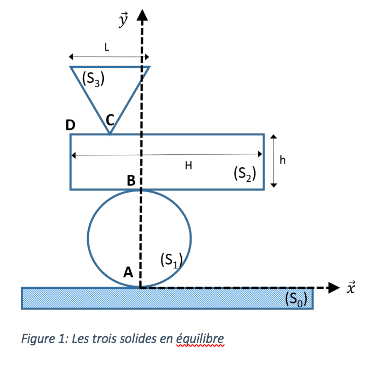
Considérons les 3 pierres comme trois solides (S1), (S2) et (S3) que l'on cherche à faire tenir en équilibre selon le schéma ci-contre (figure 1).
On considèrera le problème dans le plan (A;x ⃗;y ⃗) ainsi l'épaisseur ±e n'intervient pas. Le solide (S1) est un disque de rayon R et de masse m1, en contact avec le sol en A. Le solide (S2) est un parallélépipède de longueur H, de hauteur h, de masse m2, en contact avec (S1) en B. Enfin, (S3) est un triangle équilatéral de côté L, de masse m3 en contact avec (S2) en C.
On donne, (BC) ⃗  = -lx ⃗  + hy ⃗  et (CD) ⃗  = -dx ⃗
On rappelle que le barycentre d'un triangle se trouve au tiers de la hauteur, soit pour un triangle équilatéral à √3/6𝐿 à partir de la base.
On donne 𝜌1, 𝜌2 et 𝜌3, les masses volumiques des solides (S1), (S2) et (S3) : 𝜌1=3000kg/m3, 𝜌2=2500kg/m3 et 𝜌3=2500kg/m3.

1. Donnez la position des centres de gravité (G1) de (S1), (G2) de (S2) et (G3) de (S3).
2. On considère l'ensemble (S) constitué des trois solides (S1), (S2) et (S3). Faire le bilan des efforts extérieurs et appliquer le PFS.
3. En déduire l'expression de la réaction du sol (S0) sur (S1).
4. Donnez l'expression de la longueur l en fonction de H, d, m2 et m3.
  5. On considère que le disque est de rayon R =10cm, le rectangle est de longueur H =30cm et ⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗
de hauteur h =10cm, le triangle est de côté L =15cm. On fait varier les vecteurs 𝐵𝐷 et 𝐶𝐷 tels que l =7,55cm et d =5cm (figure (a)) et l =4,5cm et d =10cm (figure 2(b)). Vérifiez dans les cas (a) et (b) si l'équilibre des pierres est conservé. Proposez une solution géométrique qui permet de conserver l'équilibre lorsque ce n'est pas le cas et précisez votre démarche ainsi que vos calculs.
⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗
6. On fait varier la géométrie du triangle en posant L =20cm. Les vecteurs 𝐵𝐷 et 𝐶𝐷 sont
définis tels que l =5cm et d =7,5cm (figure 2(c)). Les pierres sont-elles en équilibre ? Si non, proposez une solution géométrique qui permet de conserver l'équilibre et précisez votre démarche ainsi que vos calculs.
7. Calculez les coordonnées du centre de gravité G de l'ensemble (S) pour les cas (a), (b) et (c) présentés sur la figure 2. Tracez en bleu sur la figure 2 la position des centres de gravités calculés pour les trois cas (a), (b) et (c).

Je prend toute aide, conseil ou cours qui peuvent m'aider à répondre