Inscription / Connexion Nouveau Sujet
Statique des fluides - 3 liquides dasn un récipient
Bonsoir, ayant un petit partiel demain en mécanique des fluides, je m'entraine à faire des annales des années précédentes et voici un où j'aimerias savoir si mes réponses sont justes.
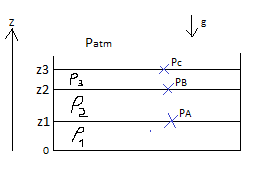
On considère un récipient au repos (Fig ci joint) contenant 3
liquides non miscibles de masse volumique 
1, 2, 3 telles que 1 < 2 < 3
1- En utilisant le principe de l'Hydrostatique, exprimer la pression dans le récipient en fonction de la position z
2- Représenter graphiquement la pression p en fonction de z
Ce que j'ai fais :
1 - Relation de l'hydrostatique : dP = -*g*dz
Il faut distinguer 3 cas : 0 
zz1, z1 zz2, z2 zz3 :
Pour 0 zz1 : P(z) = PA + 1*g*(z1-z)
Pour z1zz2 : P(z) = PB + 2*g*(z2-z)
Pour z2zz3 : P(z) = Patm + 3*g*(z3-z) (PC = Patm)
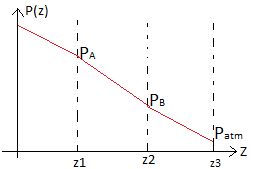
2 - Voir le graphique ci-joint
Bonne soirée,
Bonsoir
Il serait intéressant de demander à ton professeur comment il a réussi à réaliser ces 3 couches en mettant au fond le liquide le moins dense ! 
Sinon, ton étude est correcte. Je pense tout de même qu'il faut remplacer PA et PB en fonction de Patm et des données.
On a donc :
0 zz1 : P(z) = Patm + 3*g*(z3-z2) + 2*g*(z2-z1) + 1*g*(z1-z)
z1 zz2 : P(z) = Patm + 3*g*(z3-z2) + 2*g*(z2-z)
OK pour les expressions de P en fonction de z. Concernant la courbe, l'allure générale avec la continuité de P à chaque interface est bien vue.
Attentions aux coefficients directeurs des trois segments. Ce coefficient directeur est (-). Puisque, contre toute vraisemblance, le liquide le moins dense est au fond, la pression diminue plus vite entre z1 et z2 qu'entre zéro et z1 : c'est bien ce que tu as représenté ; mais elle diminue encore plus vite entre z2 et z3, ce qui n'est pas le cas sur ton graphe.
Annuler
connectez vous