Inscription / Connexion Nouveau Sujet
Spire rectangulaire
Bonjour,
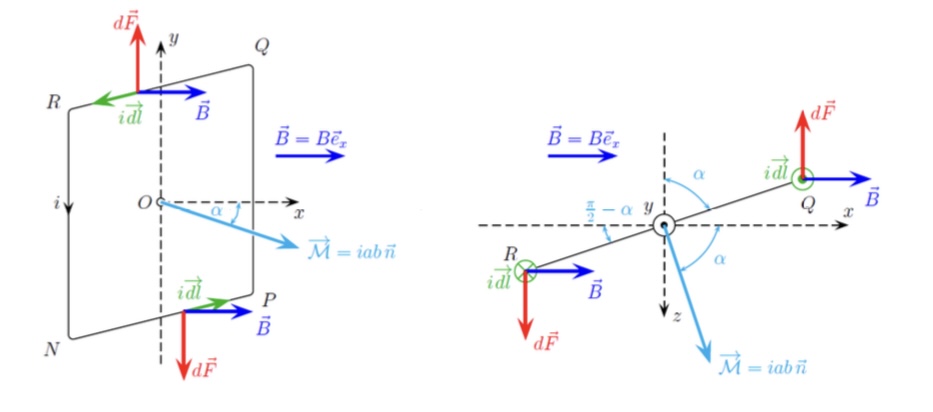
j'ai un petit problème avec cet exercice (cf image). J'ai calculé le moment magnétique résultant, j'ai . Je calcul la puissance :
. Cependant je trouve une position d'équilibre instable en
. Il me manque dont un signe moins. Mais où ? Car la spire tourne bien dans le sens direct car le moment résultant est orienté dans ce sens. Je ne comprends pas. Merci d'avance à la personne qui comprendra.
Bonjour
Ta figure me gêne un peu les angles n'y sont pas orientés. Sur la figure, supposons
>0, le couple de Laplace tend à orienter le cadre de façon que le vecteur moment magnétique ait la direction et le sens du vecteur
. Le moment du couple est alors négatif et il faut alors poser
M(F)=-i.S.B.sin()..
Ah d'accord. Comme on veut que M diminue avec , il faut prendre
, d'où le moins. Je ne sais pas si j'ai bien compris…
Et est-ce possible d'obtenir cela par le calcul ?
Ah je crois avoir compris. On peut prendre le moment positif mais par contre diminue quand
augmente, d'où le - pour la vitesse angulaire.
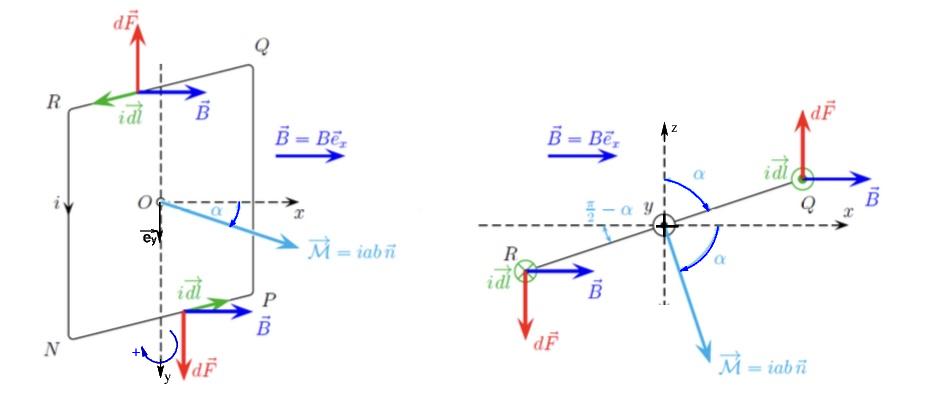
Compte tenu de l'orientation de l'axe des y vers le haut, la valeur de est négative ; cela est une source fréquente d'erreur de signes dans les problèmes. Je conseille, autant que possible, de réaliser un schéma avec un maximum de grandeurs positives, ce qui évidemment n'exclut pas un raisonnement sur les valeurs algébriques. Je me permets donc de modifier l'orientation des axes Oy et Oz de façon à obtenir sur la figure. Le moment du couple de Laplace est ainsi :
Le moment du couple de Laplace a donc comme valeur algébrique suivant (Oy) :
Lors d'une rotation élémentaire autour de l'axe (Oy) du cadre, le travail élémentaire du couple de Laplace est ainsi :
Ce travail ne dépend que de constantes et de la variable de position . Il est donc possible d'attribuer une énergie potentielle magnétique au cadre telle que :
On en déduit, à une constante arbitraire près comme pour toute énergie potentielle :
Sachant qu'un maximum d'énergie potentielle correspond à une position d'équilibre instable et qu'un minimum d'énergie potentielle correspond à une position d'équilibre stable....
Je crois que le PDF est vide…
Mais j'ai compris ! C'est parfaitement clair. Merci d'avoir pris le temps de me répondre !
le fichier du schéma ne semble pas lisible... Nouvelle tentative...
PDF - 0
Annuler
connectez vous