Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Spirale logarithme

Posté par
kamikaz 05-02-22 à 02:25

Bonjour,

Merci  d'avance.

Un point M se déplace sur la trajectoire (spirale logarithme) d'équation polaire \rho = \rho_0 e^{\theta} ; \theta = \omega t avec \omega constant.

1)

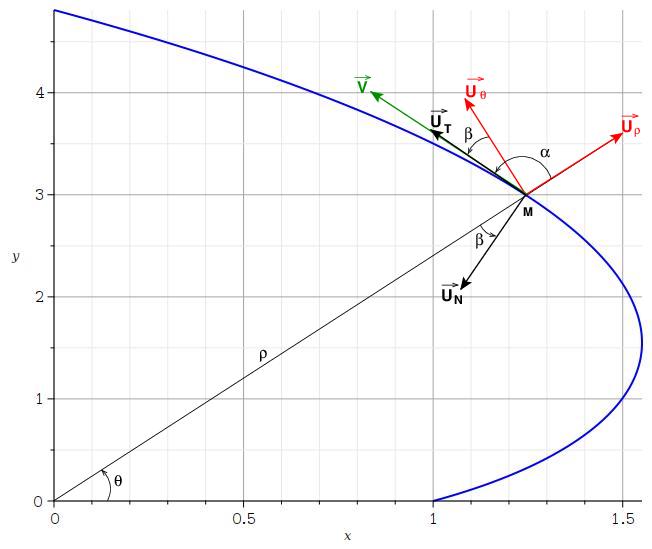
a) Dessiner schématiquement la spirale. Représenter les axes de coordonnées polaires et le repère de Frenet en un point M arbitraire de cette trajectoire.

b) Calculer les composantes des vecteurs vitesse et accélération de M en coordonnées polaires. En déduire les normes de ces vecteurs. Quelle est la valeur de l'angle entre le vecteur vitesse et le vecteur \vec u_{\rho}.

c) A partir des expressions de la composante normale du vecteur accélération, déterminer le rayon de la courbure de la trajectoire.

2) Résoudre \vec a \Lambda \vec x = \vec b

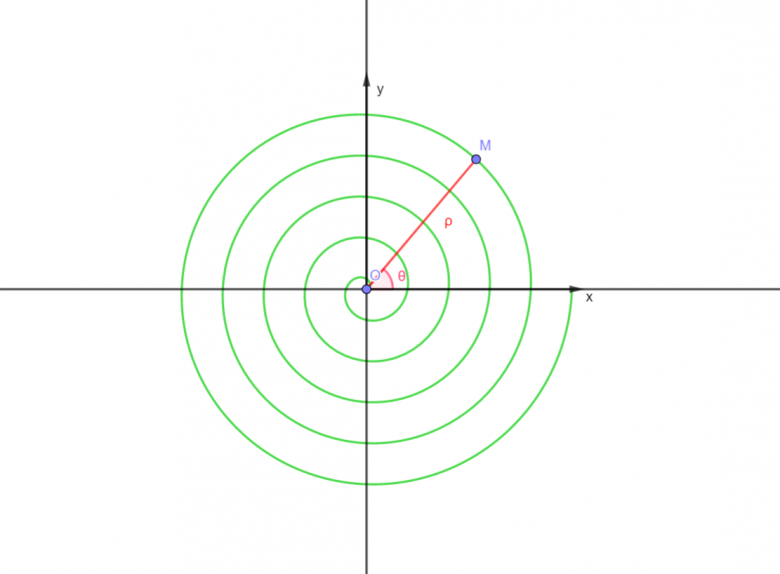
1-a) Spirale logarithme

b) \dfrac{d \vec u_{\rho}}{dt} = \theta' \vec u_{\theta} \Rightarrow \vec{V_{M}} = \begin{cases} \rho' = V_{\rho} \\\ \rho \theta' = V_{\theta} \end{cases} \iff   \vec{V_{M}} =  \begin{cases} V_{\rho} = \rho_0 \omega e^{\omega t}  \\\  V_{\theta} = \rho_0 \omega e^{\omega t}  \end{cases} \Rightarrow \vec{a} =\begin{cases} a_{\rho} = \rho_0 \omega² e^{\omega t}  \\\  a_{\theta} = \rho_0 \omega² e^{\omega t}  \end{cases}  

c) a= \dfrac{V²}{R} \Rightarrow R = \dfrac{V²}{a}

R = \dfrac{2\rho_0 \omega e^{\omega t}  }{\sqrt{\left(\rho_0 \omega² e^{\omega t}\right)²+\left(\rho_0 \omega² e^{\omega t}\right)²}} = \dfrac{\sqrt{2} \rho_0 \omega e^{\omega t} }{\rho_0 \omega² e^{\omega t}} = \dfrac{\sqrt{2} }{\omega}

2) Je ne vois pas vraiment..

Posté par
vanoisere : Spirale logarithme 05-02-22 à 10:13

Bonjour
Le vecteur x n'est pas défini par l'énoncé. Peut-être le vecteur OM.  La question aurait ainsi un rapport avec le théorème du moment cinétique...

Posté par
vanoisere : Spirale logarithme 05-02-22 à 11:31

On peut aussi imaginer que \vec x désigne le vecteur unitaire de l'axe (Ox), vecteur unitaire plus souvent noté \vec{u_x} ou \vec{e_x} ...???
\vec a désigne bien le vecteur accélération ?

Posté par
vanoisere : Spirale logarithme 05-02-22 à 13:50

Je viens d'examiner ce que tu as fait.
La figure n'est pas complète.
D'accord avec ton expression du vecteur vitesse mais pas d'accord avec ton expression du vecteur accélération. Les composantes du vecteur accélération ne sont pas les dérivées par rapport au temps des composantes du vecteur vitesse car les vecteurs unitaires \vec{u_{\rho}} et \vec{u_{\theta}} ne sont pas des vecteurs indépendants du temps. Voir ici par exemple :
En c : v2/R est l'accélération normale, pas l'accélération...

Posté par
kamikazre : Spirale logarithme 05-02-22 à 17:47

Citation :
\vec a désigne bien le vecteur accélération ?


Oui oui

Posté par
kamikazre : Spirale logarithme 05-02-22 à 17:49

Enfin.. je pense. Mais l'énoncé ne le précise pas.

Posté par
kamikazre : Spirale logarithme 05-02-22 à 18:35

Qu'est-ce qui ne va pas sur mon schéma ?

Posté par
vanoisere : Spirale logarithme 05-02-22 à 21:01

Il s'agit d'une spirale exponentielle, pas d'une spirale à pas constant. Ainsi augmente très vite en fonction de : au bout de 1 tour, =oexp(2)535o ;
au bout de 2 tours :  =oexp(4)286751o !
Personnellement, je me suis contenté de tracer la trajectoire entre =0 et =/2 avec o=1 en unités arbitraires(voir ci-dessous).
Ensuite, il faut y représenter les vecteurs  de la base polaire, un peu comme sur le schéma du  23-10-18 à 19:01 même si la trajectoire est un peu différente. base cylindro-polaire
Ensuite, il te faut revoir l'expression du vecteur accélération comme précisé dans mon message précédent.
PS : tu ne m'a pas répondu sur la signification de \vec x...

Spirale logarithme

Posté par
vanoisere : Spirale logarithme 05-02-22 à 23:31

Voici le schéma complété. J'y ai placé les vecteurs unitaires de la base polaires et les vecteurs unitaires de la base de Frénet.

Spirale logarithme

Posté par
kamikazre : Spirale logarithme 05-02-22 à 23:34

Ok, ça passe.

Merci beaucoup.

2) Je crois que j'ai trouvé..


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !