Inscription / Connexion Nouveau Sujet
Souris ficelée
Bonjour, je ne parviens pas à établir l'équation du mouvement suivant :
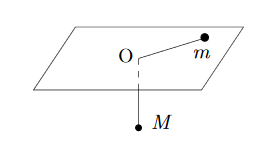
Une souris de masse m glisse sans frotter sur un plan horizontal percée d'un trou. La souris est attachée à un fil passant par le trou. L'autre extrémité du fil est liée à une masse M.
Un chat donne un coup de patte et communique initialement à la souris une vitesse orthoradiale v0. Étudier le mouvement.
Voilà je vois bien que la vitesse orthoradiale va se placer sur u
et que l'on va avoir sur l'axe z un mouvement parabolique.
Mais après avoir exprimer sur l'axe u l'accélération en coordonnées polaire j'obtiens :
2r'' + r" = cste
je ne vois pas comment intégrer la relation ensuite les deux variables étant "mobiles".
Merci d'avance pour toute aide
Bonjour
Je ne crois pas qu'il s'agisse d'un mouvement parabolique mais plutôt d'un mouvement en spirale : m tourne autour de O tandis que le fil se raccourcit.
Méthode possible : appliquer la RFD à chaque masse puis écrire que l'action du fil sur M et l'action du fil sur m sont modélisées par deux vecteurs forces de normes égales.
Sur l'axe uz, on obtient en appliquant le RFD au système composé des deux masses :
z"=-Mg/(m+M)
donc en intégrant la vitesse suivant cet axe étant nul...
je ne vois pas où je me suis trompé car effectivement votre analyse est plus que probable
Si tu orientes l'axe Oz vers le haut, le fait que le fil soit inextensible impose : z" = r"
En notant T la norme commune aux deux actions du fil sur les deux masses (l'approximation est assez moyenne car il y a sûrement des frottement au niveau du trou...) on obtient :
m(r"-r'2)=-T
Mr"=-M.g+T
addition membre à membre...
Annuler
connectez vous