Inscription / Connexion Nouveau Sujet
source de tension
Bonjour,
J'ai un petit doute sur une notion. Quand on a deux sources alternatives connectés ensemble (avec entre les deux une charge RLC), les deux sources doivent avoir la même fréquence (Ok),
mais la même phase à l'origine et la même amplitude?
Je pose cette question car la charge va modifier la phase et l'amplitude?
Merci
En fait, je dirais que si on veut ajouter une source de tension (équivalent source de tension et inductance) à une autre source, on doit vérifier que la fréquence est pareil, avec la même phase et la même tension?
Bonjour
Ton emploi de l'expression "entre les deux" me laisse supposer que tu étudies un circuit série constitué d'une seule maille.Tous les dipôles du circuit vont être parcourus par un courant de même intensité. Cependant, rien n'empêche les deux générateurs d'avoir des fém e1 et e2 d'expressions différentes : amplitudes différentes, fréquences différentes, phases initiales différentes. Pour obtenir l'expression de i(t), il suffit d'appliquer le principe de superposition :
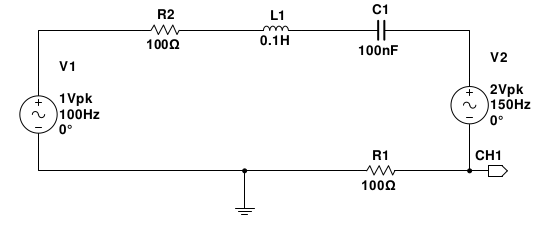
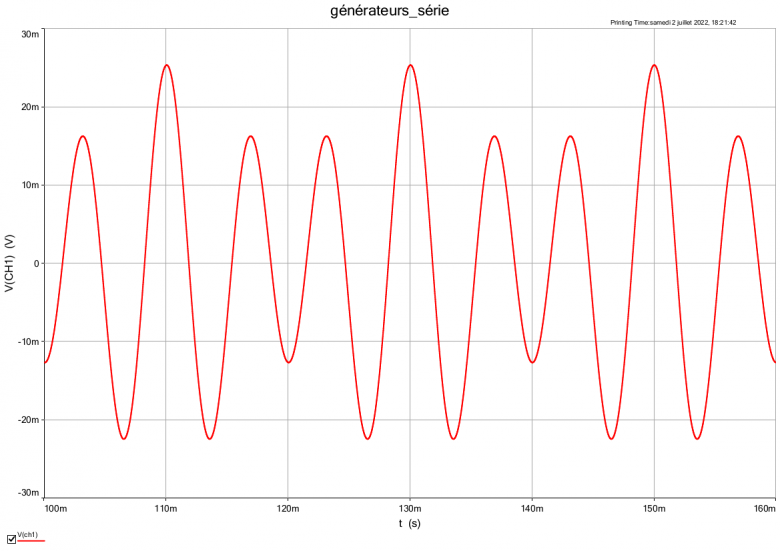
i(t)=i1(t)+i2(t) où i1(t) et i2(t) sont les intensités produites par chaque générateur séparément, le générateur éteint étant remplacé par un simple fil conducteur. Pour t'en convaincre, voici une simulation. Les caractéristiques des dipôles sont indiqués sur le schéma et la courbe représente les variations en fonction du temps de la tension aux bornes de R1, tension proportionnelle à chaque instant à l'intensité instantanée...
Si cela t'intéresse et que tu as du temps devant toi, tu peux établir l'expression de i(t) et t'auto-corriger à partir de la courbe fournie.
Merci,
Ca m'intéresse, donc je trouve Z1= R2+R1+jLw1+1/jCw1
Donc |Z1| = 15852 ohm
Z2= Z3 / Z1 avec Z3 = R1*R2 + jLw2*R1 + R1/jCw2
Donc |Z2| = |Z3|/|Z1| = 99.98 ohm
phi1 = Arg(Z1) = -90° (normal car l'impédance de la capa est énorme)
phi2 = Arg(Z2) = -0.54 ==0
Donc I = I1 + I2 = |V1|/|Z1| sin(w1*t - phi1) + |V2|/|Z2| sin(w2*t-phi2)
Pourquoi on peut pas prendre I = I1-I2 ? (comment on sait en fait ?)
I1eff = 1/15852*sqrt(2) == 0 A
I2eff = 0.0141 A
Ieff = (comment calculer au fait car ce n'est pas I1eff + I2eff...)
Ya surement une erreur car le signal I1 est nul pour moi...
Ensuite pour avoir votre courbe on fait I*R1 (complexe).
Ah j'allais oublié pour I, on ne peut pas additionner les complexes de I1 et I2 car ils ont une pulsation différente? C'est cela?
Peut être mon erreur vient de Z2 car R2+ jLw2 + 1/jCw2 et R1 ne sont pas en parallèle mais série ...(le problème vient de la masse, je vois mal...)
D'accord avec tes résultats concernant i1(t). J'obtiens :
Z1=15854
; 
1=-1.558rad (valeur très proche de -90° comme tu l'as remarqué) ; ce qui conduit à :
i1(t)=I1m.sin(
1t-1)
i1(t)=6,31.10-5sin(200
t-1,56) (en ampère)
J'avais oublié de préciser que mon logiciel utilise les sinus plutôt que les cosinus pour les valeurs instantanées :
v1(t)=V1m.sin(1.t) ; v2(t)=V2m.sin(2t)
En éteignant le premier générateur et en allumant le second, le circuit est exactement le même mais il est orienté en convention générateur si on conserve pour i2 le même sens que pour i1 :
Z2=-R1-R2-j(L12-1/(C12))
Je te laisse terminer.
Au fait : comment obtenir très simplement la valeur théorique de la période de i(t) ? (à vérifier à partir de la courbe...)
Merci,
(Il n'y a pas une erreur dans sin(200pi*t-1.56), mais plutôt sin(200pi*t+1.56) ?)
Donc dans le premier cas on était en convention récepteur.
L'impédance est négative car comme en continu on a u=-Ri en convention générateur? donc on dit que =
?
Z2 = 10518 ohm
phi2 = 91.09°
i2(t) = 1.9*10^-4 * sin(300pi*t-91°)
Donc comme on a orienté dans le même sens les courants, on a
i(t) = i1(t) + i2 (t)
Pour le moment je n'ai pas d'idée... un indice ?
J'ai trouvé une méthode sur internet avec le PPCM...
T la période de I
T1 la période de i1
T2 la période de i2
On a T= a*T1 = b*T2 car "I" périodique
T1/T2 = b/a = 1,5
Et T= PPCM(b,a) * min(T1,T2)
Mais je ne sais pas comment trouver le PPCM ...
Etourderie de ma part effectivement concernant le signe de la phase de i1(t) .OK avec ton expression de i2(t) mais attention : une phase se mesure en radians.
i2(t)=1,90.10-4.sin(300.t-1,59)
Pour l'expression de i(t)=i1(t)+i2(t), il n'y a pas beaucoup de simplification possible sauf peut-être assimiler les phases initiales à 
/2 ce qui ramène le calcul à une différence de deux cosinus. Le phénomène devient simple du point de vue calculatoire dans les deux cas suivants : f2=k.f1 avec k entier ou fréquences très proches : |f2-f1|<<f1 : on obtient alors un phénomène de battements.
La période est le plus petit réel positif tel que :
T=a.T1=b.T2 ou a et b sont deux entiers positifs.
Les deux valeurs les plus petites de a et b sont : b=3 et a=2 ce qui conduit à T=20ms ; valeur facile à vérifier graphiquement sur la simulation.
Merci beaucoup,
Oui on trouve bien 20 ms
L'impédance est négative car comme en continu on a u=-Ri en convention générateur? donc on dit que \bar{V2}=-\bar{Z2'}*\bar{i2} = \bar{Z2}*\bar{i2}
Vous avez un document sur l'association des courants efficaces? Oui cela n'a pas de sens ...
C'est juste une question de notation. J'ai utilisé la seconde mais, réflexion faite, la première est peut-être plus logique compte tenu de la convention générateur utilisée.
Les voltmètres TRMS peuvent mesurer la valeur efficace. Tu dois savoir que la valeur efficace d'une intensité périodique est la valeur quadratique moyenne calculée sur une période ou un multiple de la période. (voir éventuellement ce document (paragraphe 3) :
)
Je ne développe pas les calculs. Dans la mesure où T est un multiple de T1 et un multiple de T2, les deux premières intégrales donnent les carrés des valeurs efficaces de i1(t) et i2(t) et la troisième intégrale est nulle. Au final :
Annuler
connectez vous