Inscription / Connexion Nouveau Sujet
Solution équation différentielle d'un circuit RLC
Bonjour,
Je suis bloqué sur un exercice pour trouver la solution particulière d'une équation différentielle.
mon équa diff:
-Ewsin(wt)=CRd²s(t)/dt² + ((R/Ro)-1)ds(t)/dt + R/Ls(t)
solution homogène :
2 racines: R1= (1/2CR)*((-R/Ro)+1 +ou-sqrt( )
)
Solution particulière:
a t=0, s(t=0)=Ve(t=0)=E
et la je bloque
Merci de votre commpréhension
***Image supprimée => la recopie des 5 premières lignes de l'énoncé est obligatoire***
Bonjour
Tu es bien sûr de ton équation différentielle ? Vérifie le terme faisant intervenir (ds/dt). Ce document pourra éventuellement t'aider :
![]()
Ensuite, l'équation différentielle admet comme solution une somme de deux termes :
1° : la solution de l'équation homogène correspondant au cas particulier E=0 ;
2° : la solution correspondant au régime sinusoïdal forcé que tu peux étudier par la méthode des complexes. La méthode est expliquée dans la première partie de cette fiche mais sur un circuit différent :
![]()
J'ai oublié de le signaler dans mon précédent message : pour permettre le référencement du sujet par les moteurs de recherche (Google...), le règlement du forum demande d'écrire les premières lignes de l'énoncé tout en scannant comme tu l'as fait le schéma.
Bonsoir, merci de votre réponse, j'ai bien compris avec la solution correspondant au régime sinusoïdal forcé. Cependant mon ami vient de me dire que je n'avais pas les droits de l'image donc si vous le permettez, je vous prie de bien vouloir supprimer mon 1er message avec l'image. Merci d'avance pour votre compréhension et votre assistance. Cordialement
Bonjour,
 extrait de
extrait de Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?
Si tu veux éviter les pbs de droits d'auteur, dans ce cas je te demande malgré de refaire le schéma électrique (manuscrit, paint ...) pour que ce sujet ne devienne pas complètement incompréhensible et de recopier l'énoncé comme demandé par vanoise.
Merci
Concernant la solution particulière correspondant au régime sinusoïdal forcé, tu obtiens le résultat "de tête" si tu as remarqué :
L.C. 2
2 1 et si tu connais les propriétés du circuit "bouchon" (L//C).
1 et si tu connais les propriétés du circuit "bouchon" (L//C).
La solution correspondant au régime transitoire est étudiée en détail sur le premier document indiqué précédemment.
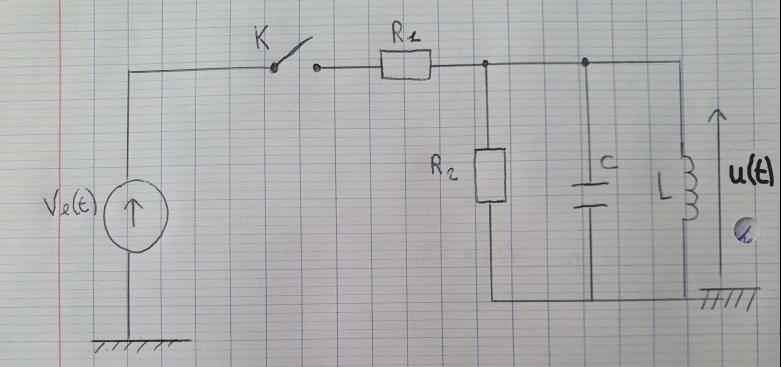
A t=0s l'interrupteur K se ferme
Le circuit était au repos quand K s'est fermé
1) Exprimer l'équation différentielle relative au circuit selon u(t)
2) Chercher u(t) avec les conditions initiales
La loi des nœuds, nous donne :
i(t)=i1(t)+i2(t)+i3(t)
i1(t)=u(t)/R2
i2(t)=C*du(t)/dt
i3(t)=1/L  u(t)dt
u(t)dt
et i(t)=(Ve(t)/R1) - (u(t)/R1)
et en dérivant selon dt on obtient l'équa diff:
(dVe(t)/dt)/R1)=C(d²u(t)/dt²) + ((1/R2)+(1/R1)du(t))/dt + (1/L)*u(t)
2) On cherche la solution homogène et la solution particulière
et s(t)=sh(t) + sp(t)
Voila
D'accord : tu as réglé l'erreur de signe.
sp(t) est la solution en régime sinusoïdal forcé. La solution est évidente si tu remarque que, puisque L.C. 2=1, l'association en parallèle (L//C) possède une impédance infinie et se comporte en circuit "bouchon". sp(t) a donc la même expression qu'en enlevant L et C du circuit.
2=1, l'association en parallèle (L//C) possède une impédance infinie et se comporte en circuit "bouchon". sp(t) a donc la même expression qu'en enlevant L et C du circuit.
sh(t) est la solution correspondant au régime transitoire, elle s'obtient en posant E=0 dans les calculs. Comme sur le document que je t'ai fourni, tu as intérêt à écrire l'équation différentielle sous la forme :
Dans ce problème :  =
= o...
o...
Bonjour, je tiens à m'excuser pour le temps entre nos messages,
Je voulais juste vérifier si tout était en ordre concernant les conditions initiales.
avec vos documents, on a :
continuité des tensions:
u(t<0)=u(t=0)=0 car condensateur déchargé
iL(t<0)=iL(t=0)=0
De plus iR0(t=0)=0 car u(t=0)=0
donc i(t=0)=iC(t=0)=E/R1
D'accord avec ton dernier message. Pour résoudre l'équation différentielle dont sh(t) est solution, tu as aussi besoin de connaître .
pour la dérivé de
je sais déjà que
donc
je dérive ma solution de l'équation différentielle
et après j'arrive à trouver mes constantes d'intégrations
ensuite je dois tracer une courbe de u(t) de t=0s jusqu'au régime permanent mais je vois pas comment faire
déja ma solution c'est : u(t)=A1 exp(r1t) + A2 exp(r2t) - Ksint(wt)
r1 et r2 <0 donc ma courbe est selon -ksin(wt)
je suis censé trouver une courbe sinusoïdal ?
Concernant sp(t) : il s'agit de la solution en régime sinusoïdal établi. Comme déjà expliqué, tout se passe comme si L et C étaient enlevés. Le circuit se comporte en diviseur de tension :
D'où la solution générale :
En remarquant : R1<<R2, on constate que la solution en régime sinusoïdal établi est très proche de ve(t).
On peut poser : et
, faisant ainsi apparaître deux constantes de temps
 1 et
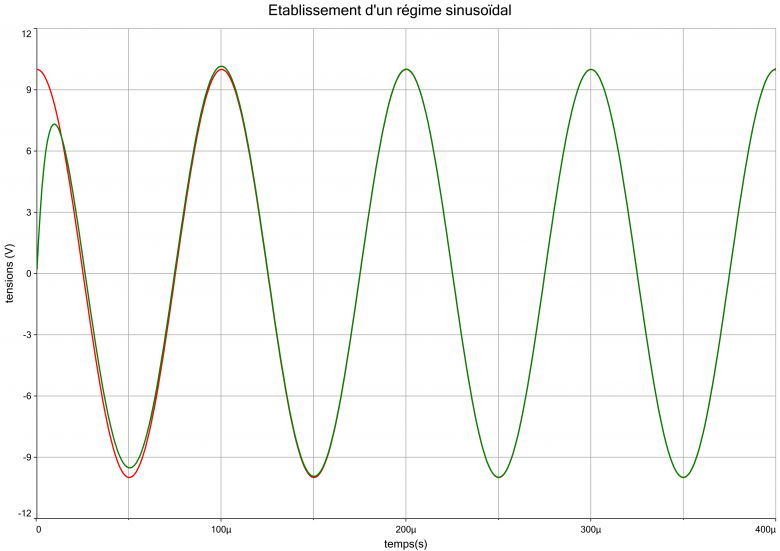
1 et  2 qui se trouve deux valeurs inférieures à la période du régime sinusoïdal. Conséquence : au bout d'une période et demie environ, la solution sh(t) correspondant au régime transitoire est devenue totalement négligeable et ne reste que la solution sinusoïdale correspondant au régime sinusoïdal. C'est pour cette raison que, dans de nombreux problèmes, on se contente d'étudier le régime sinusoïdal établi sans étudier le régime transitoire compte tenu de sa durée très courte.
2 qui se trouve deux valeurs inférieures à la période du régime sinusoïdal. Conséquence : au bout d'une période et demie environ, la solution sh(t) correspondant au régime transitoire est devenue totalement négligeable et ne reste que la solution sinusoïdale correspondant au régime sinusoïdal. C'est pour cette raison que, dans de nombreux problèmes, on se contente d'étudier le régime sinusoïdal établi sans étudier le régime transitoire compte tenu de sa durée très courte.
Évidemment ici, le cas est très particulier puisque la solution sinusoïdale est très proche de la tension d'entrée, tu as un cas un peu plus général sur le document que je t'ai fourni.
Illustration de tout cela ci-dessous où la courbe rouge correspond à ve(t) et la courbe verte à u(t). Bien visualiser les deux courbes au voisinage de t=0 puis constater que les deux courbes se confondent pratiquement pour t >1,5T environ.