Inscription / Connexion Nouveau Sujet
Solide autoporteur (deux ressorts)
Bonjour ,
Merci d'avance. 
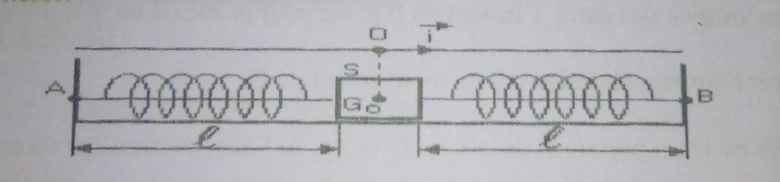
Deux ressorts identiques de masse négligeable, sont accrochés à un solide autoporteur S qui repose sur une table parfaitement plane et horizontale.
Les deux ressorts sont fixés en A et B aux extrémités de la table. On tire le solide S suivant la droite AB d'une distance d=12.5 cm et on le lâche sans vitesse.
On donne :
• masse du solide autoporteur : M=560 g ;
• longueur à vide des ressorts: l0=15 cm ;
• longueur des ressorts lorsqu'ils sont accrochés à S : l=30 cm ;
• raideur d'un ressort : k=7,2 N/m.
1) Etablir l'équation différentielle du mouvement.
2) Calculer la période des oscillations du solide S.
3) Calculer sa vitesse maximale.
4) Calculer l'énergie mécanique de l'oscillateur.
Réponses
1) 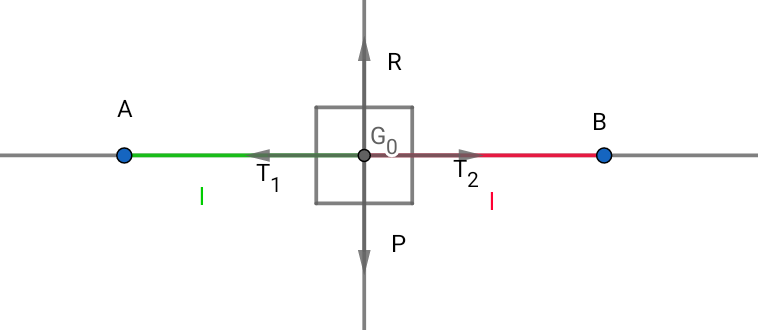
Système : le solide autoporteur S.
Référentiel : Terrestre supposé galiléen.
Bilan des forces : le poids du solide ;
La réaction du support ;
La tension du fil (côté gauche) ;
La tension du fil (côté droit).
Application du théorème du centre d'inertie.
Projection dans la base (Ox ; Oy) :
On sait que T=kx en général mais ici je ne vois pas vraiment comment faire pour trouver la valeur de x.
Bonjour
Quand un ressort se comprime, l'autre se dilate et inversement...Il faut faire une figure avec x différents de zéro (x>0 par exemple) et bien réfléchir au sens des deux forces
L'expression de la tension d'un ressort fait intervenir la différence entre la longueur à la position d'abscisse x et la longueur à vide lo... Il te faut donc réfléchir aux expressions des longueurs des deux ressort quand G a pour abscisse x...
Go est le milieu du segment (AB) : chaque ressort possède alors un allongement (l-lo). T1 et T2 sont deux forces qui se compensent. Le solide est à l'équilibre. Suppose que tu déplace le centre G d'une distance x dans le sens positif. L'allongement du ressort de gauche devient alors (l+x-lo) et l'allongement du ressort de droite devient alors (l-x-lo). Les deux tensions ne sont plus égales. Que devient l'expression de la somme vectorielle ?
Deux méthodes :
déduire l'équation horaire x=f(t) de l'équation différentielle et en déduire l'expression de la vitesse...
ou bien raisonner sur la conservation de l'énergie mécanique.
Vu l'ordre des questions, il est peut-être plus logique d'utiliser la première méthode.
L'équation horaire des deux ressorts est de la forme :
Xm=d= 0,125 m.
k= 7,2 N/m
m= 560 g = 0,56 Kg
Le problème maintenant c'est le
Tu peux aussi écrire la vitesse :
En raisonnant sur les valeurs de x et de v à la date t = 0, tu peux obtenir les valeurs de Xm et de  .
.
L'énergie mécanique est ici la somme de l'énergie cinétique et des énergies potentielles élastiques des deux ressorts. Elle est constante au cours du mouvement en absence de frottement. Le plus simple est de la calculer à l'instant initial car dans ce cas, l'énergie cinétique est nulle. L'énergie potentielle de pesanteur est constante puisque l'altitude de G reste fixe. On peut donc arbitrairement la choisir nulle.
D'accord , mais je croyais qu'il n'y avait pas de hauteur ici.
Puisque on a affaire à deux horizontaux ici.
Puisque on a affaire à deux horizontaux ici.
C'est bien ce que j'ai expliqué dans mon précédent message à propos de l'énergie potentielle de pesanteur mais il faut tenir compte des énergies potentielles élastiques des deux ressorts.
mais il faut tenir compte des énergies potentielles élastiques des deux ressorts.
Pourquoi ?
Peut être que je confonds mais quelle est la différence entre l'énergie potentielle de pésanteur et l'énergie potentielle élastique ?
L'énergie potentielle de pesanteur est l'énergie potentielle associée au poids. Elle vérifie la relation :
Puisque l'altitude reste fixe, le poids ne travaille pas. Il n'y a pas de variation d'énergie potentielle de pesanteur. Inutile donc de faire intervenir cette énergie potentielle : on peut la choisir nulle puisque tu sais que l'énergie potentielle est toujours définie à une constante arbitraire près.
En revanche, les tensions des deux ressorts travaillent. Il faut leurs associer une énergie potentielle. Revois ton cours sur le sujet : l'énergie potentielle d'un ressort de raideur k, de longueur à vide Lo et de longueur L possède l'énergie potentielle : . Si on adapte aux notation de ton problème et si on note :
l'allongement de chaque ressort à l'équilibre, l'énergie potentielle des deux ressorts s'écrit :
Je te laisse simplifier et terminer. Tu peux relire mes messages précédents pour mieux comprendre.


