Inscription / Connexion Nouveau Sujet
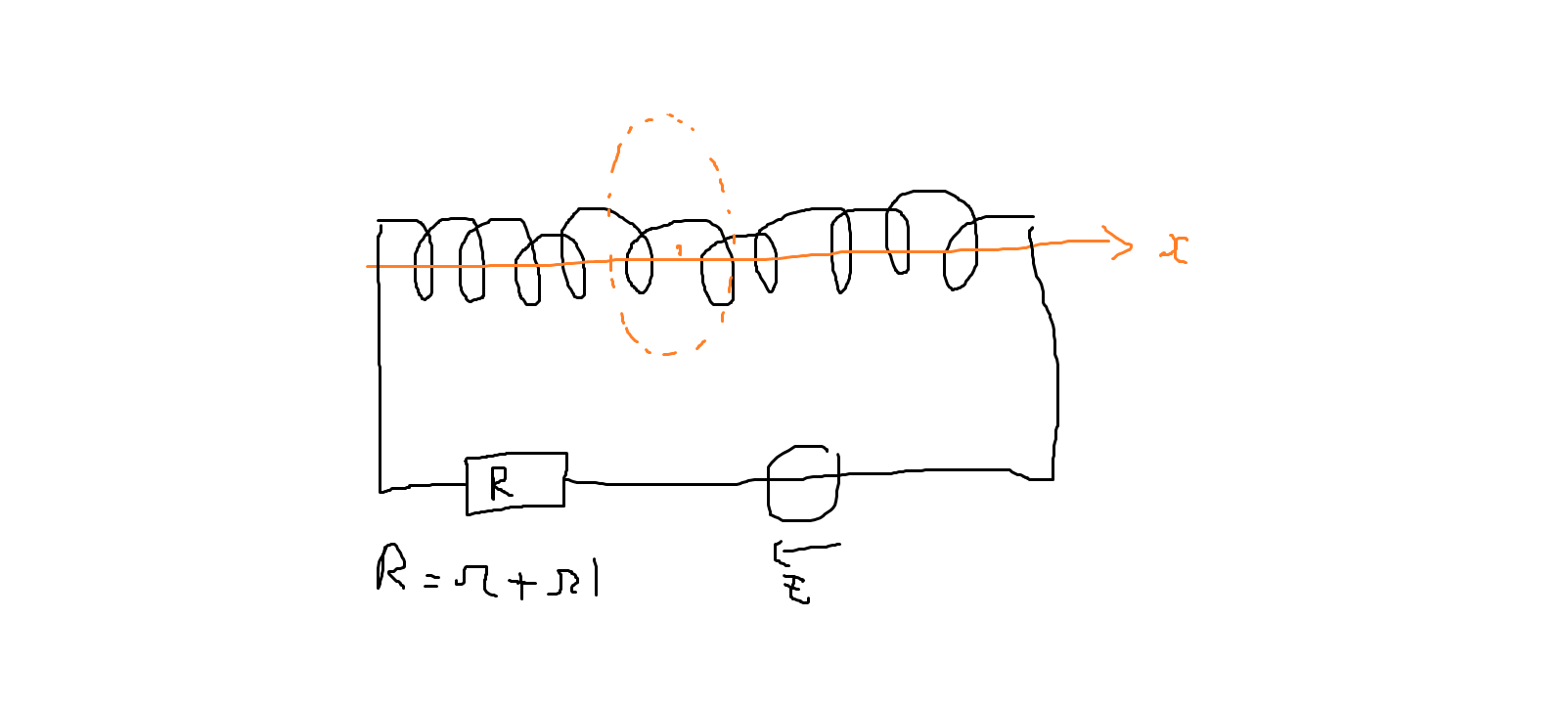
Solénoïde à l'intérieur d'une spire
Bonjour,
Comme dit dans le titre, on prend un solénoïde de rayon constitué de
spires par unité de longueur. Le solénoïde est alimenté par une fem E. On connaît aussi la résistance interne du générateur
et la résistance du solénoïde
. On place autour du solénoïde une spire de rayon
tel qu'on peut le voir sur le schéma (de même axe). On connaît aussi
.
Le but est de déterminer le plus à travers la spire externe. Je n'y arrive pas car on ne connaît pas le nombre de spires dans le solénoïde, ni la longueur du solénoïde. On a que . Du coup je ne vois pas trop comment aboutir... Et je ne vois pas non plus comment faire intervenir les paramètres électriques. Si quelqu'un peut m'apporter une indication. Merci.
Bonsoir
En très bonne approximation, le champ magnétique créé par le solénoïde est uniforme à l'intérieur de celui-ci et nul à l'extérieur.
La surface du disque délimitée par la spire peut se décomposer en deux parties :
1° : un petit disque de rayon R1 où le champ magnétique est uniforme et égal à celui créé par le solénoïde ;
2° : le reste de la surface où le champ magnétique est nul.
Le calcul du flux magnétique est donc très simple. Attention tout de même aux signe de ce flux : il dépend du sens du courant dans le solénoïde , de l'enroulement du fil constituant le solénoïde et du sens de circulation choisi pour la spire. Tout cela doit être clairement indiqué sur un schéma propre.
Bonsoir,
Sans fournir de schéma pour le moment et en raisonnant en valeurs absolues si besoin, on a que .
Avec ceci je trouve le bon résultat (les valeurs numériques de tous les paramètres intervenant dans cette précédente expression sont fournis par l'énoncé, et l'application numérique est donnée, celle-ci correspond à la mienne). À quoi cela sert-il de donner R2 ? En fait c'est un peu bizarre car mon expression est indépendante de R2 alors qu'intuitivement il semble que R2 a une importante influence.
À quoi cela sert-il de donner R2 ? En fait c'est un peu bizarre car mon expression est indépendante de R2
Certains concepteur d'énoncé fournissent volontairement des données concernant une situation physique qui sont inutiles dans la résolution. Cela devrait à mon avis se faire plus souvent : c'est une très bonne façon de tester la solidité des connaissances des étudiants et leur sens critique.
alors qu'intuitivement il semble que R2 a une importante influence
Le flux magnétique à travers une surface quelconque se calcule par la relation :
où
Si tu augmentes la surface concernée dans une région de l'espace où


