Niveau maths spé

Solenoide

Posté par
jonus 20-02-13 à 20:46

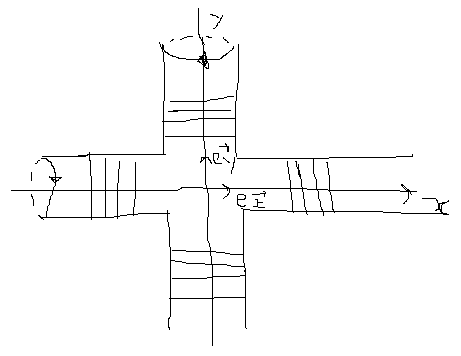
En faisant abstraction des spires manquant dans la partie centrale, le montage cidessous est considéré comme un ensemble de deux solénoïdes infinis et identiques, disposés
dans le vide de sorte que leurs axes soient perpendiculaires et concourants en leur milieu O.
Chaque solénoïde est composé d'un enroulement pratiquement circulaire, réalisé sur un
cylindre très long de rayon R, comportant N spires jointives par unité de longueur. Le
solénoïde d'axe Ox est parcouru par un courant d'intensité i1(t), celui d'axe Oy est parcouru
par un courant d'intensité i2(t). L'orientation des conducteurs est indiquée sur la figure n° 1.On pose : i1(t) = Im cos(ωt)
i2(t) = Im cos(ωt+θ)
1.On pose θ=Pi/2. Montrer que le champ magnetique en tout point de la partie centrale est telle que B(t)=Bo.u(t) (B(t) et u(t) vecteurs), ou Bo ne depend pas du temps et ou u(t) est un vecteur unitaire du plan(ex,ey) (ex, ey vecteurs), tournant a une vitesse dont on precisera le vecteur.

Solenoide

Posté par re : Solenoide 21-02-13 à 20:06

je connais le champ d'un solenoide mais apres (uoNi)

Posté par re : Solenoide 21-02-13 à 20:06

merci de votre aide

Posté par re : Solenoide 21-02-13 à 20:36

Bonsoir,
1)
$\vec{B_1}(t)\,=\,\mu_0\,N\,I_m\,cos(\omega\,t)\,\vec{e_x}$

$cos\left(\omega t\,+\,\frac{\pi}{2}\right)\,=\,-\,sin(\omega t)$

$\vec{B_2}(t)\,=\,-\,\mu_0\,N\,I_m\,cos(\omega\,t\,+\,\frac{\pi}{2})\,\vec{e_y}\,=\,\mu_0\,N\,I_m\,sin(\omega\,t)\,\vec{e_y}$

$\vec{B}(t)\,=\,\vec{B_1}(t)\,+\,\vec{B_2}(t)\,=\,\mu_0\,N\,I_m\,cos(\omega\,t)\,\vec{e_x}\,+\,\mu_0\,N\,I_m\,sin(\omega\,t)\,\vec{e_y}$

$\vec{B}(t)\,=\,\mu_0\,N\,I_m\,\left(\,cos(\omega\,t)\,\vec{e_x}\,+\,sin(\omega\,t)\,\vec{e_y}\,\right)$

On peut poser : $B_0\,=\,\mu_0\,N\,I_m$
et :
$\vec{u(t)}\,=\,cos(\omega\,t)\,\vec{e_x}\,+\,sin(\omega\,t)\,\vec{e_y}$ qui est un vecteur unitaire parce qu'il est de norme égale à 1 ==> $||\vec{u(t)}||\,=\,\sqrt{cos^2(\omega\,t)\,+\,sin^2(\omega\,t)}\,=\,\sqrt{1}\,=\,1$ et il tourne à la vitesse $\omega$

Donc $\vec{B}(t)$ peut se mettre sous la forme :
$\vec{B}(t)\,=\,B_0\,\,\vec{u(t)}$
avec $B_0$ indépendant du temps et $\vec{u(t)}$ , vecteur unitaire tournant à la vitesse $\omega$ .