Bonjour
Tout dépend de la précision souhaitée...
Je note  (r,) les coordonnées du centre d'inertie de la terre dans un repère héliocentrique.
Si tu considères que la distance entre les deux centres est suffisamment grande devant les dimensions des deux astres, tu peux considérer que le champ gravitationnel créé par le soleil est radial indépendant de et quasi uniforme au niveau de la terre (effet de marée négligé). L'étude se mène comme si le soleil était assimilé à une boule. Le mouvement du centre d'inertie G de la terre est le même qu'avec un soleil assimilé à une boule. Le théorème de König n° 2 permet d'affirmer que le moment cinétique en G de la terre, mesuré dans un repère géocentrique est un vecteur constant. Si la terre est assimilée à un carré, il faut effectivement utiliser sa matrice d'inertie pour exprimer son moment cinétique.
Une étude rigoureuse est beaucoup plus complexe et demande une simulation informatique. Le champ gravitationnel créé par le soleil au niveau de la terre n'est pas uniforme et dépend de r et de . On peut imaginer de découper le soleil en 100² petits carrés dont les coordonnées dans le repère héliocentrique peuvent facilement être exprimées qi le centre du soleil à pour coordonnées (0,0). Tu divises de même la terre en 100² carrées élémentaires dont les coordonnées cartésiennes peuvent être déterminées en faisant intervenir celles du centre de la terre.
Chaque carré élémentaire est alors soumis à 100² forces gravitationnelles dont tu peux calculer la résultante et le moment résultant en G. Puis tu sommes les résultantes et les moments résultants sur les 100² carrés élémentaires de la terre. Tu auras ainsi la résultante de l'action du soleil sur la terre et le moment résultant en G de cette action... Ayant le torseur des actions en G exercées par le soleil sur la terre, on peut en déduire le mouvement...
Tout cela n'est pas très simple... L'astronomie avec des astres quasi sphériques n'est déjà pas simple, alors...

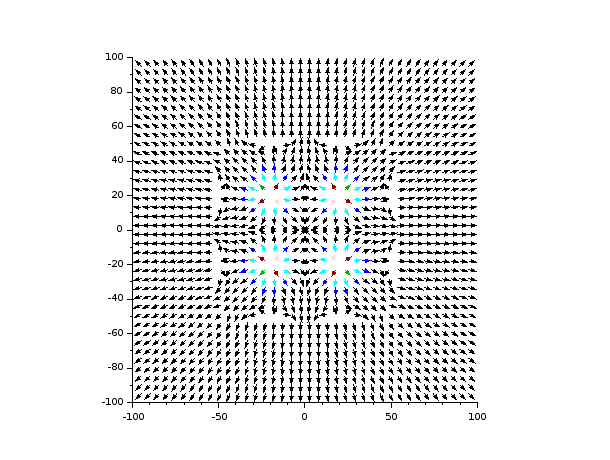
Je ne sais pas si tu te sens toujours concerné par ce problème. A tout hasard, voici une petite simulation informatique où la direction et le sens du vecteur champ gravitationnel  créé par un "soleil carré" sont visualisés par de petites flèches régulièrement réparties dans le plan d'étude (il ne s'agit pas de lignes de champs). J'ai  supposé l'astre homogène, centré à l'origine du repère avec une longueur de côté égale à 100 (unité arbitraire).
Sur la première figure, j'ai étudié le vecteur champ dans le carré et à son voisinage immédiat. On voit que la structure du champ est assez complexe à l'intérieur du carré mais on retrouve quand même les fondamentaux : le vecteur champ est colinéaires aux  axes de symétrie de la source (axes du repère et diagonales).
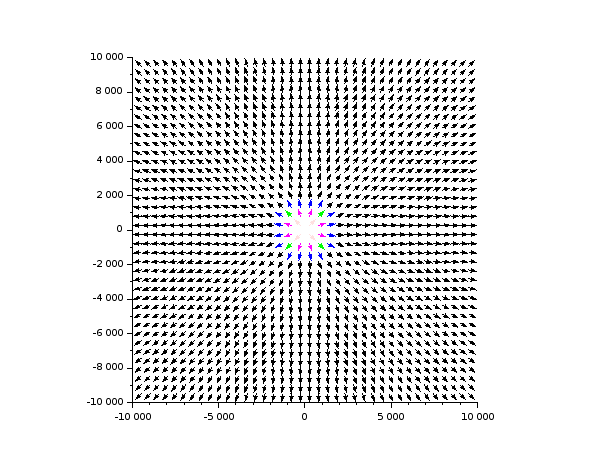
Sur la seconde figure, j'ai étendu l'étude à des coordonnées de valeurs absolues maximales 100 fois supérieures à la longueur du côté de la source dans la mesure où la distance entre le centre du soleil et le centre de la terre est environ 100 fois le diamètre du soleil. On remarque bien que, loin de la source, le vecteur champ gravitationnel est radial centripète, ce qui semble valider l'étude simplifiée proposé par mon premier message.

Merci pour tes réponses et tes simulations !

Oui j'aimerais plutôt étudier ces effets à "courtes" distances. Donc si je veux faire ça, pas le choix, il faut que je prenne en compte la résultante des forces de gravitation sur chaque points de la planète. Ça risque d'être gourmand en calculs !