Il faut lire (n+1/2)T dans l énoncé de la consigne, désolé

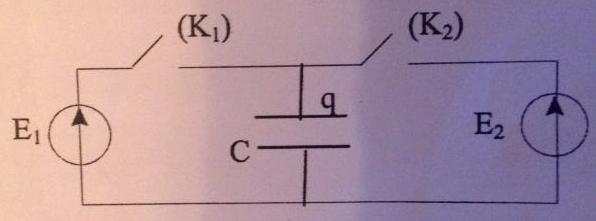
Je vois l exercice comme ceci :

Au tout début le condensateur était déchargé, du coup pendant un temps T/2 il a été chargé.
Ensuite cest K2 qui a été ouvert et K1 fermé. Et du coup ça dépend des cas, soit le condensateur a pas été chargé entièrement donc il continue à se charger, soit il est chargé complètement et il va se décharger ....

Devons nous alors prendre l initiative de se dire que vu que q(t) est périodique, alors quand K1 est ouvert et K2 fermé, le condensateur subi une charge complète et dans l autre cas une décharge complète et ainsi de suite ??

PS: la consigne en entier est : déterminer et tracer l évolution de q(t) sur une période. On posera a=T/(2RC) et on prendra T=10microsecondes R=100ohms C=10nF E1=5V et E2=1V

Merci d avance

Commence par écrire sans faute (et sans oublier les parenthèses nécessaires) la partie :

— si nT < t < ( n+ 1/2)T, l'interrupteur K1 est fermé   tandis que K2 est ouvert (n est entier relatif).
— si  (n+ 1/2)T < t < (n + 1)T, l'interrupteur K1 tandis que K2 est fermé.

Désolé :/

Help

K1 fermé et K2 ouvert.

i = (E1 - u)/R = C du/dt
RC du/dt + u = E1

u(t) = E1 + A.e^(-t/(RC))

Avec la condition initiale U(0) = Uo -->

Uo = E1 + A et donc A = Uo - E1

u(t) = E1 + (Uo - E1).e^(-t/(RC))

u(T/2) = E1 + (Uo - E1).e^(-T/(2RC))
-----
K1 ouvert et K2 fermé.

Je remets l'horloge à 0 au moment de la commutation des contacts pour faciliter les calculs.

Ici, la condition initiale est U(0) = [E1 + (Uo - E1).e^(-T/(2RC))]

i = (u - E2)/R = -C du/dt
RC du/dt + u = E2

u(t) = E2 + B.e^(-t/(RC))

u(0) = E1 + (Uo - E1).e^(-T/(2RC)) --> B = E1 + (Uo - E1).e^(-T/(2RC)) - E2

u(t) = E2 + (E1 + (Uo - E1).e^(-T/(2RC)) - E2).e^(-t/(RC))

u(T/2) = E2 + (E1 + (Uo - E1).e^(-T/(2RC)) - E2).e^(-T/(2RC))

u(T/2) = E2 + (E1 + (Uo - E1).e^(-T/(2RC)) - E2).e^(-T/(2RC))

Et on est revenu comme au début de mon intervention, donc on doit avoir :

E2 + (E1 + (Uo - E1).e^(-T/(2RC)) - E2).e^(-T/(2RC)) = Uo

D'où on peut tirer Uo ... (en posant -T/(2RC) = a : )

E2 + (E1 + (Uo - E1).e^-a - E2).e^-a = Uo
E2 + E1.e^-a + Uo.(e^-a)² - E1.(e^-a)² - (e^-a).E2 = Uo
Uo(1-(e^-a)²) = E2.(1-(e^-a)) + E1.(e^-a).(1-(e^-a))
Uo(1+(e^-a)) = E2 + (e^-a).E1
Uo = (E2 + (e^-a).E1)/(a(e^-a)+1)

Donc avec K1 fermé et K2 ouvert, la tension u du condensateur varie de (E2 + (e^-a).E1)/((e^-a)+1) jusque E1 + (Uo - E1).(e^-a) (avec Uo = (E2 + (e^-a).E1)/((e^-a)+1)

et avec K2 fermé et K1 ouvert la tension u du condensateur varie de E1 + (Uo - E1).a jusque (E2 + (e^-a).E1)/((e^-a)+1) (avec Uo = (E2 + (e^-a).E1)/((e^-a)+1)
------------------------
Avec a=T/(2RC) et on prendra T=10microsecondes R=100ohms C=10nF E1=5V et E2=1V

a = 10^-5/(2*10^-8*100) = 5

Uo = (E2 + e^-a.E1)/((e^-a)+1) = 1,0268 V

Avec K1 fermé et K2 ouvert, la tension u du condensateur varie en 5 µs de (1,0268 V jusque E1 + (Uo - E1).e^-a = 4,973 V)

et avec K2 fermé et K1 ouvert la tension u du condensateur varie en 5 µs de 4,973 V jusque 1,0268 V

On peut faire le tracé à partir des u(t) déterminés avant.

Aucun calcul vérifié.

Sauf distraction.  

Bonjour et Merci beaucoup J-P !
En fait je croyais que l enoncé disait que dans tous les cas, dans tel circuit, la charge etait tout le temps periodique peut importe les conditions initiales sur la charge du condo.... Mais en fait pas du tout il faut se servir du fait quon nous dise que c est periodique pour determiner la bonne condition initiale sur la charge de C. Merci encore et bon dimanche

Ah daccord ! Cest interressant alors ce circuit ...

Aussi l exercice me demande de calculer les valeurs moyennes de l intensites du courant parcourant les 2 interrupteurs.
Donc si je me fie a la formule pour une fonction periodique qui est 1/T
Alors je trouve que pour l un ca fait 1/T(q(T/2)-q(0)) et pour l autre ca donne 1/T(q(T)-q(T/2)) donc on aurait <i1(t)>=-<i2(t)>, est ce bon ? Ca me parait bizarre....

Courant dans K1 :

i = C.du/dt
Avec u(t) = E1 + (Uo - E1).e^(-t/(RC))
i(t) = -C.(Uo-U1)/(RC).e^(-t/(RC))
i(t) = (U1-Uo)/R .e^(-t/(RC))

  (avec Uo = ce qui a été trouvé dans les réponses précédentes)
-----
Même principe pour le courant dans K2.

Sauf distraction.  

Daccord merci J-P !
Mais du coup quest ce qui ne va pas avec ce que jai marque lors de mon dernier message ?? Je ne vois pas l erreur ....

En gros je dis que pour le courant dans k1 :
la valeur moyenne vaut 1/T(q(T/2)-q(0)) avec la formule trouvee dans les questions precedentes
Et pour le courant dans k2 je fais de meme en utilisant 1/T(q(T/2)-q(0)) avec la formule trouvee dans le deuxieme cas... et du coup vu que q(T/2) du premier cas=q(0) du deuxieme et que q(0) du premier cas vaut q(T/2) du deuxieme, je trouve des valeurs d intensite moyennes opposees ...

Dailleurs meme avec ce que vous avez dit on trouve que integrale de i =C*u
Donc on a bien
i moy= 1/T*C*(u(T/2)-u(0))
Non ?

Dans ma réponse précédente, remplacer U1 par E1.


La valeur moyenne d'un courant dépend de sa "forme" et pas seulement de ses valeurs en 0 et T/2 (par exemple)

Pour le courant moyen dans K1 (via l'intégrale que j'ai donné) :

im = 1/T * (E1 - Uo)/R * (RC) * [e^-t/(RC)](de 0 à T/2)

im = 1/T * (E1 - Uo)/C * [e^-T/(2RC) - 1]

im = 1/T * (E1 - Uo)/C * [e^-a - 1]

Avec Uo = (E2 + e^-a.E1)/((e^-a)+1)

...

Sans vérification. (A toi de le faire)
-----
Et on trouvera aussi, que les courants moyens dans K1 et K2 sont de mêmes valeurs mais de signes opposés... ce qui est d'ailleurs évident sans calculs (puisque c'est un cycle)

Daccord merci beaucoup !
La derniere question est quelle resistance faudrait il placer entre les deux sources pour avoir le meme courant moyen ?
Une resistance infinie non ?

Bizarre cette question, à part avoir un courant moyen nul je ne vois pas ce qui pourrait faire l affaire...

Pour le courant moyen , dans ce cas, on pouvait le faire sans intégrale.
------------------------

"La derniere question est quelle resistance faudrait il placer entre les deux sources pour avoir le meme courant moyen ? "

Ici, il faut comprendre, je pense, "même courant moyen dans les sources de tension.

Sur le dessin du haut :

Le courant moyen dans C est évidemment nul, mais pas dans les sources de tension, avec E1 > E2, le source E1 fournit un courant de charge de C (celui qui passe dans K1) et la source E2 un courant de décharge de C (celui qui passe dans K2)

Soit I1 et I2 les moyennes de ces courants.

Tu as trouvé justement que I2 = -I1 (en valeurs moyennes) et tu en as calculé les valeurs.

I1 et I2 ne sont évidemment pas nul ... c'est (I1 + I2) qui est nul (donc le courant moyen dans C)
-----

La dernière question te demande (sur le dessin du bas), la valeur du R à mettre pour que I ait la même valeur que la valeur moyenne I1 du dessin du haut.



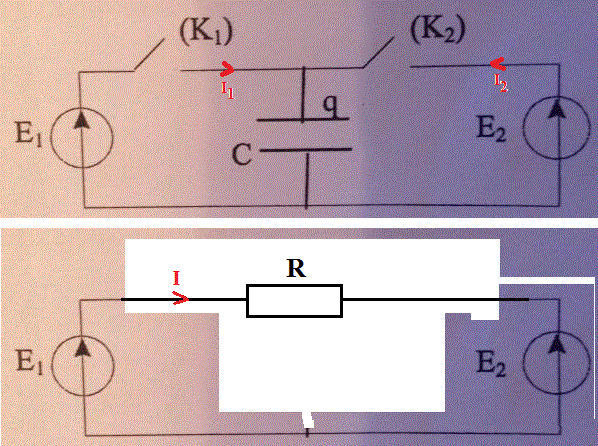
Sauf distraction.  

Ah daccord ! Il suffit simplement d isoler R en faite dans l expression i=U/R=i1 moy sur votre schema.  Merci bien en tout cas, je commencais a en avoir marre de cette question ^^ . Bonne journée