Bonjour,

Il faut intégrer l'équation différentielle, ce que vous ne faites pas : imaginez que l'équation soit , vous écrivez
ligne 1 : v[0]=0
ligne 2 : v[1]=0
ligne 3 : v[2]=-(v[1]-v[0])/k*0.01
On voit bien que cela ne résout pas l'équation.

On transforme l'EDO en , ce qui donne


Un lien vers qqch de plus explicite en terme de cellule de tableur.

Ceci étant, je répète ce que j'ai dit sur un autre site, pourquoi ne pas utiliser un langage de programmation qui serait lisible et comporterait des bibliothèques d'intégration d'EDO.

Re bonjour ^^

Je ne comprends pas bien.
A la ligne 3 je fais (v[1]-v[0])/0.001   (0.001 c'est le pas de temps)
Ça correspond bien à (v[i]-v[i-1])/dt ?
Enfin je fais plutôt v[i-1]-v[i-2]/dt parce que je ne connais pas encore la valeur actuel de v[i] puisque je cherche à la calculer.
Si je commence par
ligne 1 : v[0]=0
ligne 2 : v[1]=0
c'est juste parce que pour une simulation numérique il faut bien des conditions initiales et je m'attendais qu'en mettant 0;0 et qu'après quelques valeurs improbables  les résultats finissent par converger vers des valeurs plus justes.

OK pour Excel.

qqch qui aurait du vous mettre la puce à l'oreille, vous avez une EDO d'ordre 1, donc une  condition initiale et là vous en avez besoin de deux. Votre technique ne résout pas l'équation différentielle.

Prenons comme exemple , avec v(0)=0, de solution connue .
Vous écrivez , on prendra A=1, k=1, deltat=1
1 v=0
2 v=0
3 v=1-(0-0)/1
dès la première ligne de calcul, on est déjà sur l'asymptote.

Le lien donné 17/02 06:31 explicite la méthode à suivre paragraphe 2.2 page 2.
En quoi la méthode proposée vous pose problème ?

Merci
J'ai enfin essayé la méthode du pdf et ça marche. Même si j'ai pas compris pourquoi ma méthode à moi ne marche pas. ^^
Je reviendrais si j'ai d'autres questions sur mon "projet".

Bonjour,

Très bien.
Je ne sais pas comment vous faire comprendre le problème de votre méthode :
permet à un instant t de calculer l'accélération en fonction des données à cet instant, soit
Mais pour calculer ce qui se passe à l'instant suivant, vous avez bien besoin de calculer v(t+dt) à partir de v(t), et cela c'est la définition même de l'accélération : .
Tant que vous n'avez pas v(t+dt), vous ne pouvez pas calculer

Bonjour

Je m'y suis remis et là je constate qu'en faite la simulation arrête bien de donner des erreurs mais qu'à la place elle donne des valeurs bizarres au bout d'un moment. Et ça bien avant que le volume d'eau = 0.
Et je vois aussi qu'en raison de la nouvelle méthode, ce qui se passe pour Uout dépend fortement de la valeur initiale puisqu'on intègre. Mais je ne connaît pas cette valeur initiale et du coup j'ai mis une formule ultra simplifié que j'ai trouvé dans un autre document : Uout(0)=RACINE(2P). Et celle ci donne seulement une approximation de Uout. Je ne sais pas quoi mettre d'autre...

Je sais pas si ça fait partie du problème mais je me demande aussi a quel moment il vaut mieux prendre des valeurs de la ligne d'au dessus et à quel moment il vaut mieux prendre celles de la même ligne.
Par exemple pour la force de poussée à la case J4, vaut t-il mieux écrire :
=$B$16*(PI()*($B$8/2)^2)*I3^2
ou
=$B$16*(PI()*($B$8/2)^2)*I4^2
?
Y a t-il une règle particulière ?

Je poste les captures actualisés de ma simulation. J'espère qu'elles sont lisibles.

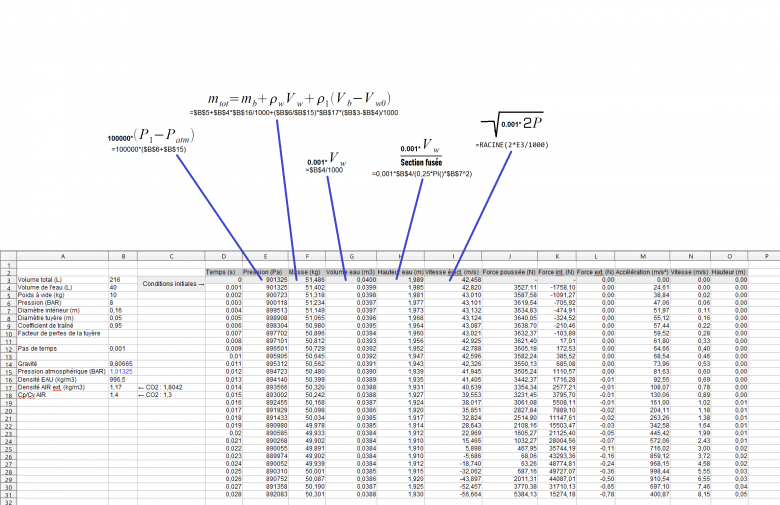
Juste pour dire que je regarde de près, mais il y a déjà le fait que vous utilisez une méthode d'Euler, la plus simple (et compréhensible) des méthodes d'intégration et il est connu que cette méthode est instable.
Vous pouvez essayer de diminuer le pas.

Pour ce qui des règles de calcul des cellules d'Excel, je ne sais pas.

Pour ce qui est de Uout, si vous prenez l'équa diff., à l'instant initial, la vitesse est nulle (avant que le bouchon saute, l'eau est au repos).

La formule simple néglige le transitoire, vous pouvez éventuellement l'appliquer à la place  de votre équa diff ; avec vos valeurs, j'ai trouvé un transitoire de 0,02s.

C'est quoi exactement dans l'équation qui correspond au transitoire ? Si c'est le terme avec la dérivé ça pourrait bien m'arranger.

J'ai essayé avec Uout(0)=0 et là ça m'a l'air de donner des valeurs plus correctes, seulement en négatif. C'est pas si con que ça parce que le jet d'eau part dans le sens opposé de celui de la fusée. Mais du coup il y a des problèmes de signes ailleurs puisque la quantité d'eau augmente. J'ai alors refait la simulation en inversant le signe de Uout, et là comme par magie j'obtiens des résultats correctes qui se rapprochent à 15% près de résultats que donnent d'autres simulateurs.
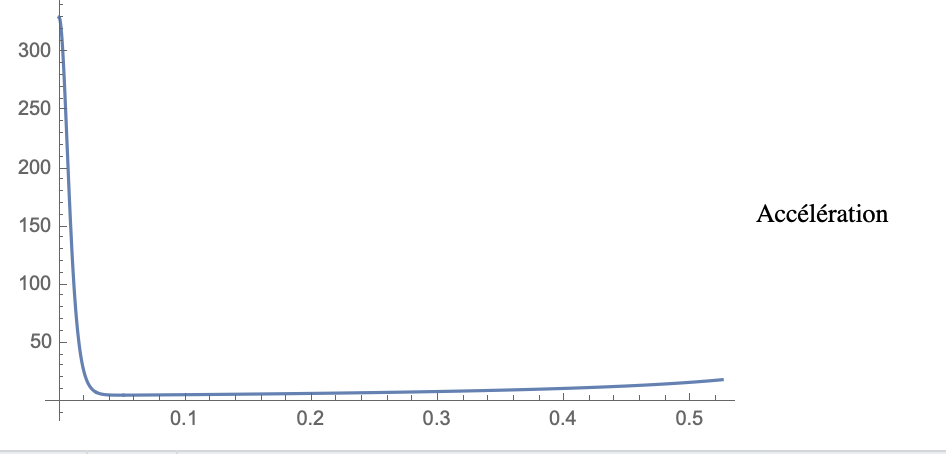
Par contre l'accélération fait des choses très bizarres, parce qu'elle commence par partir dans le sens opposé pendant un moment assez significatif.
A partir du moment où l'eau dans la fusée approche 0m^3 la simulation explose. C'est moins grave puisque je m'arrête à ce moment là.
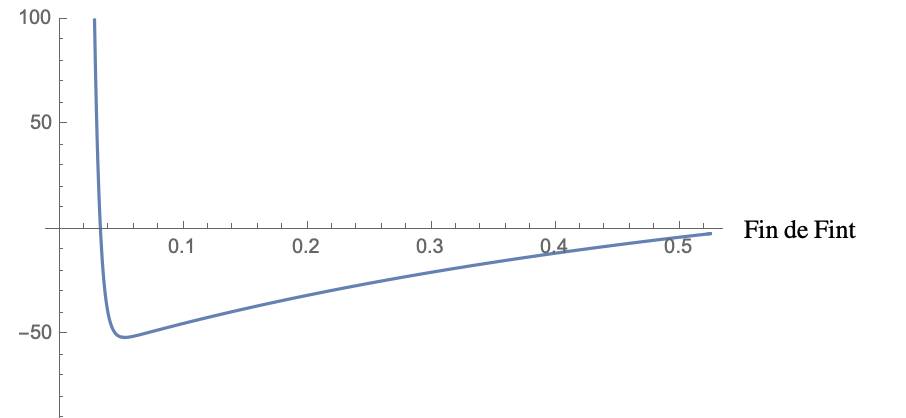
Je poste les courbes de Uout et l'Accélération que j'ai obtenu avec un pas de 0.001 et 0.0001.

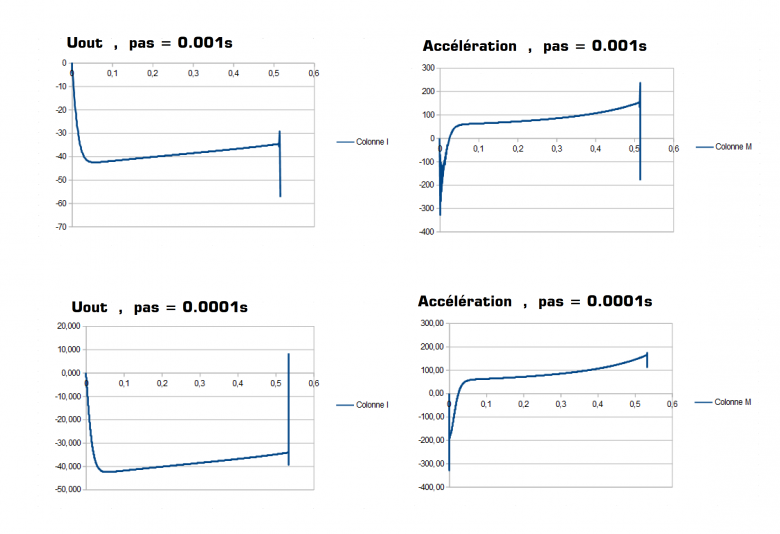
Cela m'a l'air bon !

Pour uout, je trouve la même chose, y compris pour le transitoire.

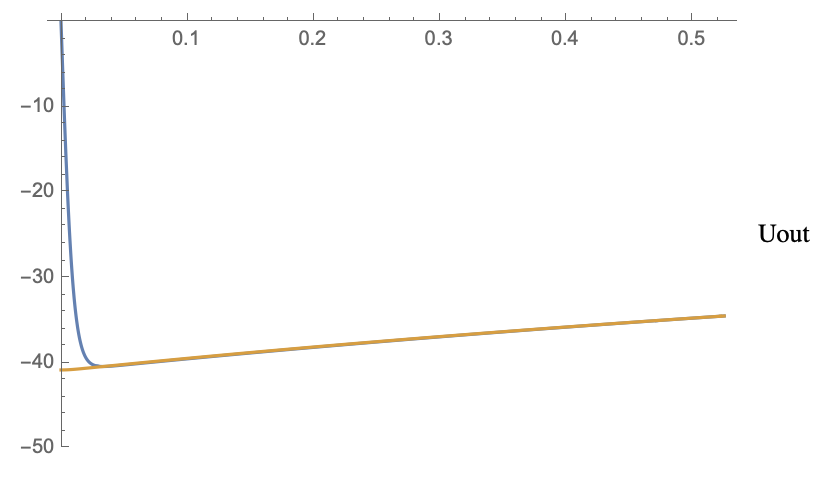
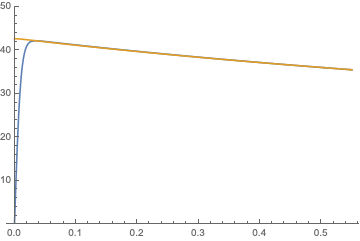
Le transitoire correspond à l'équation dUout/dt. J'ai comparé les deux calculs, cela donne :

La courbe bleue est avec equa diff, la marron avec Uout(0)=RACINE(2P)+terme de pesanteur (autrement dit l'équa diff dans laquelle on considère que dUout/dt=0), on voit qu'il n'y a un écart que lors des premières 20 ms.

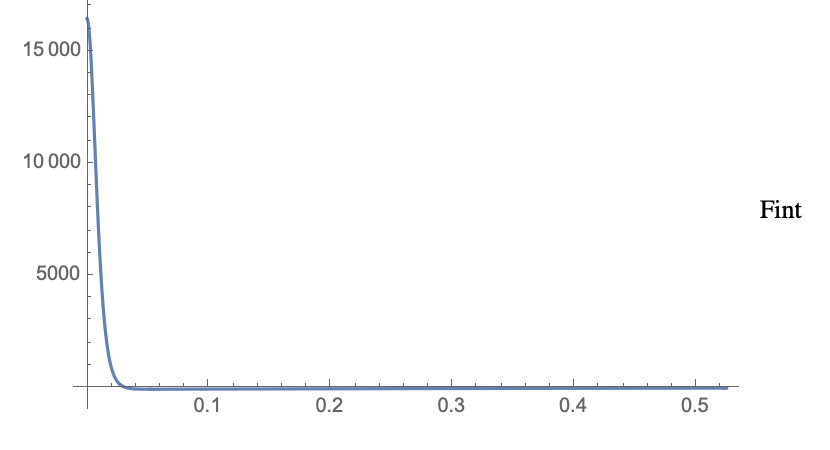
Pour l'accélération, le problème vient du Fint qui domine au début. Je pense que le problème est que l'accélération calculée n'est pas celle de la fusée, mais du centre d'inertie G de celle-ci, or durant le transitoire la fusée ne décolle pas (puisque Uout est trop faible), mais l'eau qui est éjectée fait baisser G. Je vais voir si on peut corriger les équations.

Autrement dit, pour faire disparaitre le pb d'accélération négative, vous pouvez soit négliger le transitoire, soit calculer l'accélération de la coque de la fusée.

Cela revient à négliger le transitoire.

J'ai refait les calculs à ma manière avec dV/dt (V  vitesse de la coque) et j'obtiens la même équation (même correctif par rapport à la formule classique), donc la formule complète prend en compte à la fois le transitoire et le déplacement de l'eau, contrairement à ce que j'ai pensé au début (message du26/03) .  

Avec transitoire, quels sont les signes de u, du/dt, Fint, Fthr et idem après ?

Des mesures dispo ici :



Cela confirme un pic d'accélération au démarrage (mais dans l'autre sens, donc signe à vérifier), par contre, il y a une phase que je ne comprends pas : "on tube"

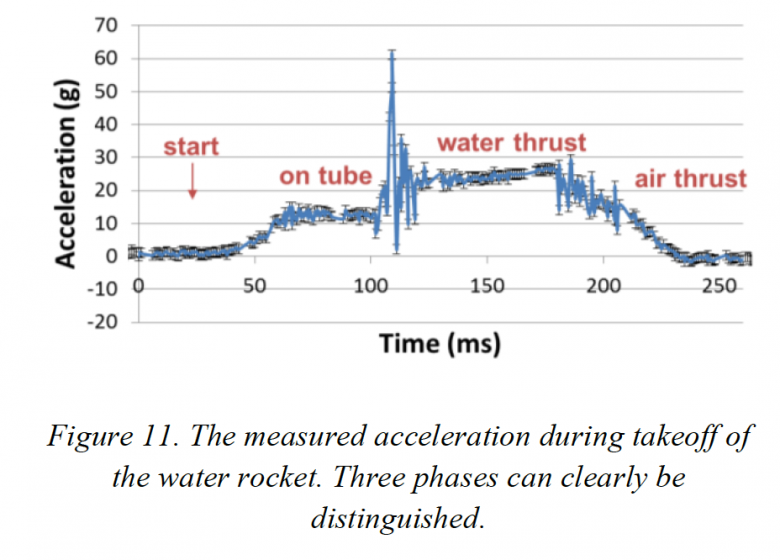
Oui, sur la photo le start est "coupé".

Pour la phase on tube: On peut aidé la fusée au décollage en la faisant glisser sur un tube attaché au lanceur.
Voilà un exemple :
https://upload.wikimedia.org/wikipedia/commons/6/6e/Lanceur_fusee_eau_colliers.jpg

Premières courbes : Fint, Fint avec zoom sur la fin, accélération.

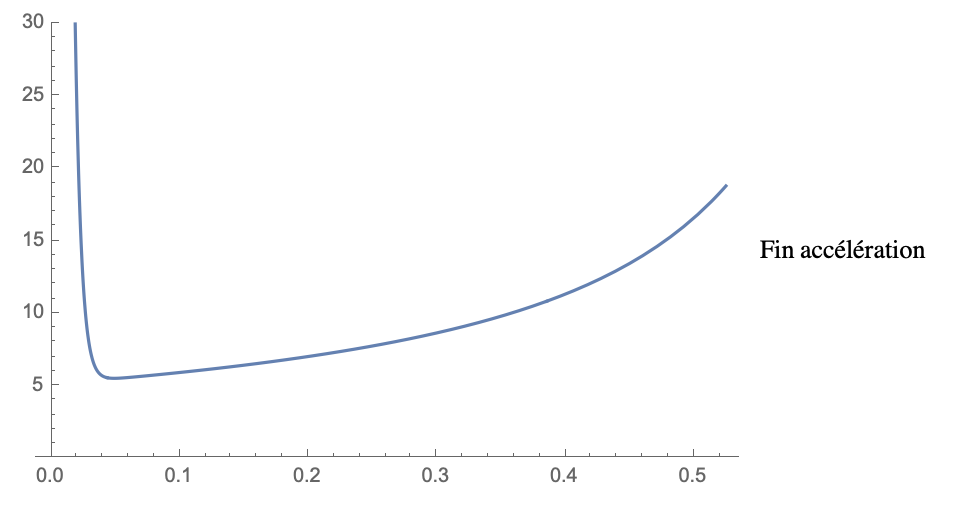
Suite des courbes : zoom sur la fin d'accélération, Uout.

Mes courbes sont algébriques (donc la vitesse d'éjection négative). On voit que dans le transitoire du/dt<0, ce qui conduit à Fint>0 puis qu'ensuite Fint<0.

Au vu de vos signes, j'ai l'impression que vous avez "redressé" u (>0), mais que par contre le du/dt est algébrique. Donc à mon avis, le signe à vérifier est celui du terme en du/dt de Fint (il devrait y avoir un signe moins conduisant à un Fin>0).