Inscription / Connexion Nouveau Sujet
Signaux physiques
Bonsoir à tous,
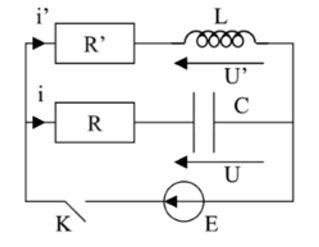
Voila l'exercice que j'ai à faire :
On considère que le générateur est déchargé. A t=0, on ferme l'interrupteur.
Le but est de donner les valeurs des courants i et i' et des tensions U et U' lorsque t=0+ et t=+ .
.
Puis de donner les expressions de i'(t) et U(t).
J'ai commencé par faire une loi des mailles, soit
U'+ R'I'=E Pour la grande maille
U+RI=E Pour la petite maille
Je me suis placée en convention récepteur.
Pour la petite maille on a U+RC(dU/dt) =E
Soit dU/dt+ U/ = E/
= E/
Ensuite je ne sais pas vraiment quoi faire, je ne sais pas si je suis sur la bonne piste.
Je vous remercie d'avance pour votre aide.
Bonjour,
Tu dois intégrer l'équation différentielle du premier ordre que tu viens d'obtenir. Tu lèves l'ambiguïté sur la constante en considérant qu'un condensateur assure la continuité de la tension à ses bornes à la date t = 0.
Méthode analogue pour l'autre maille mais cette fois-ci il faudra considérer que la bobine assure la continuité de l'intensité dans sa branche à la date t = 0.
Pour l'autre maille on obtient
U'+R'I'=E
LdI'/dt + R'I'=E
dI'/dt+ R'I'/L=E/L
dI'/dt+ I'/ =E/L
=E/L
I'(t)= E/R'(1-exponentielle de (-t/ '))
'))
"On considère que le générateur est déchargé."
Je présume qu'on doit remplacer ton "générateur" par "condensateur."
On te demande de donner les valeurs des courants i et i' et des tensions U et U' lorsque t=0+ et t=+oo.
Ceci ne nécessite absolument pas d'écrire des équations différentielles, mais juste de comprendre physiquement ce qui se passe en se basant sur :
- Il n'y a jamais discontinuité de courant dans une inductance.
- Il n'y a jamais discontinuité de tension aux bornes d'un condensateur
- En régime établi, et avec des circuits ne comprenant que des générateurs de tension continues constantes, un condensateur se comporte comme un circuit ouvert et une inductance se comporte comme un court-circuit.
Personnellement, si tu arrives à répondre en étant obligé de te servir d'équations différentielles, c'est à dire se cacher derrière des calculs au lieu de comprendre physiquement les phénomènes qui se passent dans ce circuit, tu devrais être sanctionné.
Mais ce n'est que mon avis.

Effectivement je me suis trompée c'est le condensateur qui est déchargé.
Je suis désolée mais même avec les précisions que vous avez apportées je ne comprends pas les phénomènes qui se passent dans le circuit.
On a U'=LdI'/dt
Donc I'= U'/L
U'/L
On a U= Q/c
Et I= dQ/dt
Est ce que c'est ça et après je dois le faire pour t=0 et t=+ ?
?
Je t'aide pour l'instant t = 0+
En t = 0-, donc juste avant de fermer le contact K, on a i' = 0
Comme il ne peut y avoir de discontinuité dans le courant passant dans une inductance, on a aura i'(0+) = i'(0-)
---> i' = 0 en t = 0+
La différence de potentiuel aux bornes de R' est donc nulle en t = 0+ ---> U' = E
En t = 0-, donc juste avant de fermer le contact K, on a U = 0
Comme il ne peut y avoir de discontinuité dans la tension aux bornes d'un condensateur, on aura U(0+) = U(0-)
---> U = 0 en t = 0+
La différence de potentiel aux bornes de R est donc E en t = 0+ ---> i = E/R
-----
Essaie de réfléchir pour trouver ce qui se pesse si t --> +oo
...
Sauf distraction. 
Merci beaucoup,
Pour t-->+ , est ce que j'ai le droit de me servir du fait que le condensateur se comporte comme un interrupteur ouvert et que la bobine se comporte comme un fil?
, est ce que j'ai le droit de me servir du fait que le condensateur se comporte comme un interrupteur ouvert et que la bobine se comporte comme un fil?
Dans ce cas la, on peut dire que i'=0 pour t-->+ Puisque une fois que le courant est établi, la bobine se comporte comme un fil.
Puisque une fois que le courant est établi, la bobine se comporte comme un fil.
Puis on peut dire que i=0 pour t-->+ Puisque une fois le courant établi, le condensateur se comporte comme un interrupteur ouvert. ?
Puisque une fois le courant établi, le condensateur se comporte comme un interrupteur ouvert. ?
Si c'est ça est ce que j'ai le droit de faire la même démarche pour U?
Pour t-->+oo, est ce que j'ai le droit de me servir du fait que le condensateur se comporte comme un interrupteur ouvert et que la bobine se comporte comme un fil?
Oui, évidemment.
Par contre une partie de ce que tu as fait dans ton post suivant est faux.
Comment peut-tu écrire par exemple que pour t--> +oo, on a i' = 0 ????
C'est faux, bien entendu, réfléchis.

Effectivement i' est différent de 0 puisqu'il augmente mais comment je trouve la valeur exacte de i quand t-->+
Pour t --> +oo, l'inductance se comporte comme un court-circuit, donc comme une résistance de 0 ohm --> U' = 0
L'impédance de la branche où passe i' est donc Z = R' + 0 = R' (pour t--> +oo)
et on a E aux bornes de R' --> i' = E/R'
---
Pour t --> +oo, le condensateur se comporte comme un court-circuit ouvert --> i = 0.
Il n'y a donc pas de différence de potentiel aux bornes de R ---> U = E
------
Sauf distraction. 


