Inscription / Connexion Nouveau Sujet
Série de Fourier/ AO intégrateur
Bonjour, pourriez-vous m'aider à comprendre la question suivante? 
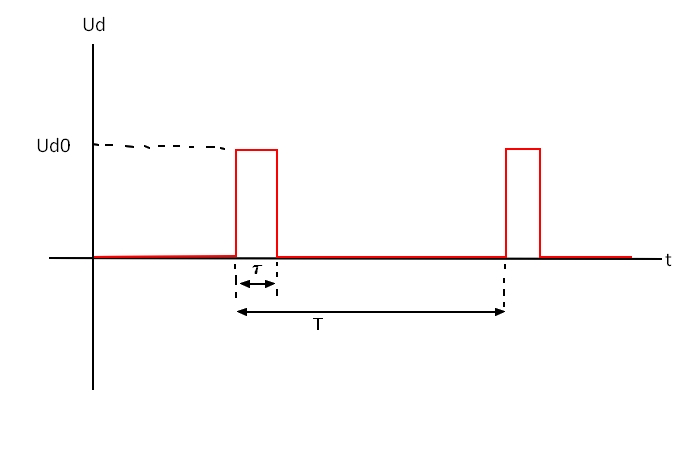
Ci-joint le graphe Ud(t) de la tension Ud, où T est la période de Ud et τ une grandeur qui nous intéresse.
On utilise un Montage à AO de type pseudo intégrateur (dans le genre: http://upload.wikimedia.org/wikipedia/commons/5/59/Active_Lowpass_Filter_RC.svg) avec en entrée Ud (Vin sur l'image) et en sortie du montage Us (Vout)
On obtient
Question: Monter qu'en choisissante judicieusement le produit R2*C on peut obtenir pour Us un signal proportionnel à τ
=> Ud est décomposable en série de Fourier Ud= <Ud> + Σ [ck* cos(2kπt/T + Ψk]
<Ud> nous intéresse car <Ud>= Ud0 * τ/T
Que faire ensuite?
Merci d'avance
Je pense qu'il faut que la tension de sortie soit continue et égale à R2/R1 <Ue> soit (R2/R1)Ud0
/T.
Donc que l'amplitude du fondamental de Us soit négligeable devant sa composante continue. Comme Us/Ue = R2/(R1
(1+R2²C²
)²) = <Us>/(1+R2²C²²)
Si R2²C²²>>1 donc si R2C <<
alors Us = Ue/R1C= TUe/2
R1C << Ud0T/. Avec Us amplitude du fondamental de uS(t) et Ue amplitude du fondamental de ue(t)
Bonjour Dilettante,
Ce que tu dis à propos de <Ud> est judicieux. Comme le mentionne Henry, détermine alors la réponse du filtre à un signal constant. Cela montrera qu'une solution au problème est que le filtre éteigne toutes les harmoniques du signal d'entrée.
Ensuite, pour déterminer la condition nécessaire, je te conseille de tracer un diagramme de Bode en amplitude. Tu y verras comment faire pour que l'harmonique de rang 1 s'éteigne. Alors, les harmoniques de rangs supérieurs s'éteindront nécessairement, d'après le diagramme.
Bon courage.
Thibault
Annuler
connectez vous