Inscription / Connexion Nouveau Sujet
Séparation isotopique
Bonsoir tout le monde,
J'ai fait un exercice de physique qui me dérange un peu car je n'aboutit pas aux résultats attendus.
Le voici : (les notations en gras designent des vecteurs)
On considère une particule de masse m et de charge q soumise a un champ magnétique uniforme B=Boex . La particule se trouve au point Mo(a,0,0) et possède une vitesse Vo= -a*Woey+
*a*Woez avec Wo=qBo/m
1) Décrire la trajectoire de la particule dans le cas où =0. Etudier qualitativement le cas où 
0
Donc quand 0, on a une vitesse perpendiculaire à B donc on aura une trajectoire circulaire dans le plan, c'est du cours...
Et qualitativement quand Vo a une composante en z on peut se dire qu'on a toujours ce mouvement circulaire poussé vers les z croissants donc un mouvement helicoidal le long de (Oz)
Celle la pas de soucis
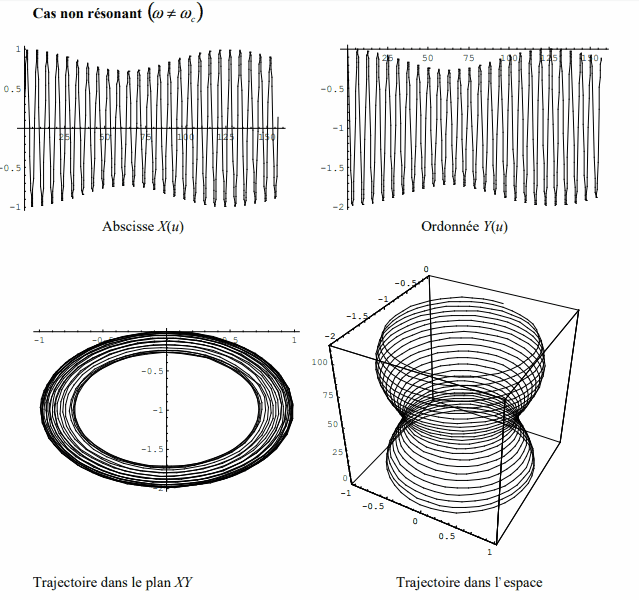
2) On superpose à ce champ magnetique un champ électrique de la forme E=Eo*cos(Wt)*ex. On suppose le regime permanent établi. Comment est modifiée la trajectoire dans le cas général où WWo ?
Là jai fait le PFD, tout ca tout ca... On se retrouve avec mdV/dt=q(E+V
B). On a B qui a une composante uniquement en z donc on a VB=VyBoex-VxBoey.
On tombe sur un systeme liant dVx/dt, dVy/dt, Vx, Vy... qui est
dVx/dt=(q*Eo*cos(Wt)/m)+(q*Bo/m)*Vy (1)
dVy/dt=(-q*Bo/m)*Vx (2)
dVz/dt=0
On utilise une methode complexe en posant u(t)=x(t)+iy(t)
(1)+i(2) 
d^2(u(t))/dt^2+(iqBo/m)*du(t)/dt=(qEo/m)*cos(Wt)
Après mon problème cest pour trouver u(t) parce que la solution générale à la rigueur c'est simple par contre la solution particulière je l'ai trouvée mais ca me fait des résultats super longs dont la représentation n'est pas en adéquation avec les réponses que je devrais avoir.
PS: je sais (normalement) quelle type de réponse je devrais avoir car l'énoncé ressemble beaucoup a une annale de concours des Mines de 2002 sauf que l'expression de E a une composante en x ET en y. Je vous joins une image des types de courbes attendues.
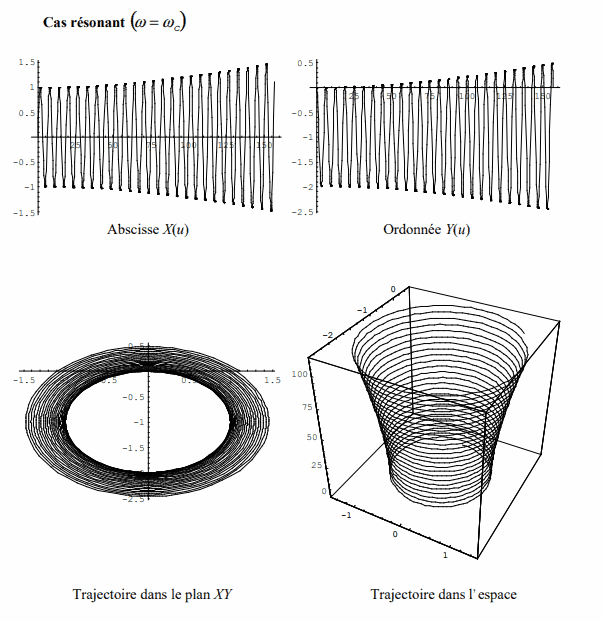
3) On s'intéresse au cas W=Wo. Montrer qu'il y a un phénomène de résonance et donner la nature de la trajectoire.
Ca simplifie un peu notre equa diff du 2) mais cest encore un peu laborieux pour ce qui est de la solution particulière...
Du coup ca serait sympa d'avoir votre aide surtout pour savoir si mon raisonnement et juste. Je m'y prend peut etre mal pour trouver la solution de l'equa diff.
Merci beaucoup d'avance !!
Bonne nuit et a demain 
Je n'ai pas vérifié l'exactitude de l'équation différentielle ...
Pour d²u/dt² + A.du/dt = B.cos(wt)
Une solution particulière est de la forme u(t) = a.sin(wt) + b.cos(wt) (1)
u'(t) = a.w.cos(wt) - b.w.sin(wt)
u''(t) = -aw².sin(wt) - bw².cos(wt)
u'' + A.u' = -aw².sin(wt) - bw².cos(wt) + A.a.w.cos(wt) - A.b.w.sin(wt)
u'' + A.u' = (-aw²- A.b.w).sin(wt) + (A.a.w - bw²).cos(wt)
On a donc le système :
(-aw²- A.b.w) = 0
(A.a.w - bw²) = B
qui résolu donne a = AB/(w.(w²+A²)) et b = -B/(w²+A²)
Et qui remis dans (1) donnent une solution particulière de l'équation d²u/dt² + A.du/dt = B.cos(wt)
u(t) = [AB/(w.(w²+A²))].sin(wt) - [B/(w²+A²)].cos(wt) est une solution particulière de l'équation d²u/dt² + A.du/dt = B.cos(wt)
Sauf distraction (pas vérifié)
Bonjour
Astuce possible pour résoudre l'équation différentielle du second ordre :
Considérer qu'il s'agit d'abord d'une équation différentielle du premier ordre dont est l'inconnue. Cela conduit à :
Déterminer A à partir des conditions initiale. Une fois l'expression de obtenue, intégrer et déterminer la constante d'intégration à partir des conditions initiales.
Mais c'est peut-être la méthode que tu as appliquée ?
Merci a vous deux pour vos reponses ! En effet, je viens de me rendre compte qu'une fois que j avais du(t)/dt je derivais au lieu d integrer !! Merci grace a vous jai trouvé mon erreur.
Passez une bonne journee
Dailleurs, en regardant votre solution particuliere vanoise, je ne pense pas quelle soit bonne car cela marcherait seulement si elle etait constante et donc ne dependait pas du temps. Or elle depend du temps.
Celle de J-P est bonne par contre.
Mais cest juste un detail, le principal cest la methode 
Annuler
connectez vous