Bonjour,

Dans la première expression de votre intégale, il y a un z à l'extérieur. Il devrait être à l'intérieur. Et les choses s'arrangent.

(intégrale, bien sur... pas intégale)

Bonjour Alban,
Mais z est une constante, donc je peux le sortir de mon intégrale?
Ou bien vous voulez parler de dz?

Tout comme ?

Sinon j'ai trouvé une autre formule de primitive:



En posant u= (x²+z²) et n= (-3/2) ?

Mais je n'y arrive toujours pas... Au secours, dès que ça se corse avec les primitives je me noie...
Blllppbbbllpppp....

Re,

Si z est un paramètre, alors que signifie le dz dans l'intégrale ? Cela doit être un dx alors ?

Et que vaut l'élément de charge qui crée l'élément de champ E que vous intégrez ensuite ?

Bref, mettes vos calculs et raisonnements depuis le début, sinon on ne verra pas où ça coince. J'ai fait un exercice du genre il n'y a pas longtemps, et je n'ai pas le souvenir qu'il y avait le moindre problème.....

Re,

En regardant votre résultat, il y a une erreur. Il faut écrire le champ élémentaire sous la forme avec M le point où vous calculez le champ et P un point de la distribution de charge, portant la charge qui crée le champ élémentaire en M.

Le problème vient du fait que vu de M, . Il faut calculer proprement ce , et les choses se débloquent.

Sauf erreur, si je traduis ton énoncé, le dz que tu as écrit dans l'intégrale devrait être dx.
Cela se trouve en remarquant la symétrie qui fait qu'il suffit de comptabiliser les composantes des champs élémentaires // à l'axe des z.
----
Et pour S dx/(x²+z²)^(3/2)

Poser x = z.t
dx = z.dt
(x²+z²)^(3/2) = z³.(t²+1)^(3/2)

S dx/(x²+z²)^(3/2) = S z/[z³.(t²+1)^(3/2)] dt

S dx/(x²+z²)^(3/2) = (1/z²) S [1/(t²+1)^(3/2)] dt = (1/z²) . t/V(t²+1)

S dx/(x²+z²)^(3/2) = (1/z²).(x/z)/V(x²/z² + 1)

S dx/(x²+z²)^(3/2) = (1/z²).x/V(x²+z²)

...

Sauf distraction.  

Bonsoir à vous,
Merci de m'accorder un peu de votre temps.
Pour vous répondre Alban, je trouve ce que vous avez écrit en projetant sur , c'est-à-dire :

Désolé pour le post précédent, j'ai eu une ambiguité de bouton
Pour vous répondre Alban, vous avez raison, j'ai bien remplacé dl par dx en me disant que que c'est un élément de l'axe Ox, 1^ère erreur...
J'ai donc refait les caculs et je trouve presque ce que vous avez écrit :
Je commence par projeter sur Ox, c'est-à-dire :



Je pose

J'obtiens

Ensuite le théorème de pythagore donne

Je l'insère dans la formule précédente

Maintenant j'intègre sur toute la longueur du segment, entre -z et z



Et c'est maintenant que je rame pour résoudre

Je propose donc

Comme je l'ai écrit plus haut avec la formule (j'espère qu'elle est correcte)

J'obtiens

Je vous épargne les détails du calcul car le résultat est totalement folklorique

Voilà, si le début de la démonstration est juste, je me retrouve bloqué à cet endroit.
Je trouve cette démonstration un peu plus compliqué que celle du disque uniformément où l'on retrouve également une intégrale mais de la forme

J'ai aussi essayé cette formule mais ça ne marche pas ici...
Je ne comprends plus rien...
La misère...

Bonsoir J-P,
Merci beaucoup pour ton aide.
Cependant, j'ai retourné ton raisonnement dans tous les sens mais je n'ai pas tout saisi.
Tu parles des champs élémentaires // Oz mais il me semble qu'ils sont tous portés par Oz au point M ?
D'où vient le principe de poser x=z.t ?
Ensuite on se sert de ?
Sur la 1^ère ligne pourquoi a-t-on le facteur z³ et pas z² ?
Ca fait beaucoup de choses à admettre mais ce qui me fait halluciner c'est que le résultat est juste, donc le problème vient bien de moi...

Je m'y remets demain,
Bonne soirée.

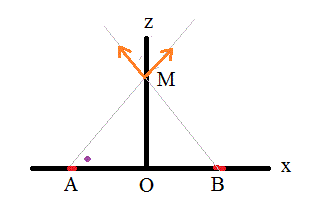
Considérons 2 segments élementaires A et B (de longueur dx) sur l'axe des x, On choisit A et B symétriques par rapport à O.

Chacun des segments élementaires (de longueur dl) porte une charge dq = Lambda.dx

Calculons les champ élémentaires en M provoqués par les dq en A et B

Avec |AO| = |OB| = |x| (qui peut varier) et OM = z (fixe)

|AM| = |BM|= V(x²+z²)

dE(en M du à A) = 1/(4Pi.€o).dq/AM² = 1/(4Pi.€o).dq/(x²+y²)

dE(en M du à B) = 1/(4Pi.€o).dq/BM² = 1/(4Pi.€o).dq/(x²+y²)

On remarquera (voir dessin) que les composantes "horizontales" de dE(en M du à A) et de dE(en M du à B) sont égales, de même direction  mais de sens contraire
---> elle se neutralisent

Par contre, les composantes "verticales" de dE(en M du à A) et de dE(en M du à B) sont égales, de même direction et de même sens (vert le haut).
---> leurs effets s'ajoutent.

La résultante des dE en M provoqués par A et B est verticale et on peut en calculer le module.

En appelant alpha l'angle repéré en mauve sur mon dessin.

On a : composante verticale du dE(en M du à A) : 1/(4Pi.€o).dq/(x²+y²) * sin(alpha) (en projetant de dE sur l'axe des z)

Mais dans le triangle AOM, on a : OM = AM.sin(alpha)
--> sin(alpha) = z/V(x²+z²)

Et donc composante verticale du dE(en M du à A) : 1/(4Pi.€o).dq/(x²+y²) * z/V(x²+z²)

On trouve pareillement : composante verticale du dE(en M du à B) : 1/(4Pi.€o).dq/(x²+y²) * z/V(x²+z²)

Et donc la résultante du champ créé en M par A et B est : 2 * 1/(4Pi.€o).dq/(x²+y²) * z/V(x²+z²)

Et avec dq = Lambda.dx

La résultante du champ créé en M par A et B est : 2 * 1/(4Pi.€o).Lambda.dx/(x²+y²) * z/V(x²+z²)

2/(4Pi.€o).Lambda.z. 1/(x²+z²)^(3/2) dx

Il suffit d'intégrer cela de x = 0 à L (pas de -L à L puisqu'on considère chaque fois des morceaux symétrique par rapport à 0 de l'axe des x)

--> E(M) = 2/(4Pi.€o).Lambda.z. S(de0àL)  1/(x²+z²)^(3/2) dx

Ce qui est équivalent à :

E(M) = 1/(4Pi.€o).Lambda.z. S(de-LàL)  1/(x²+z²)^(3/2) dx
-----

Bonjour J-P,
Tu as oublié de poster le dessin j'ai envie de dire...

WAW!
C'est super intéressant comme approche et très bien expliqué!
Néanmoins, je me permets de te demander le détail de car c'est la vraie raison de mon post.
Ta démonstration m'aide beaucoup pour la compréhension car jusqu'à présent j'enchaînais les étapes parce que "c'était comme ça" mais là c'est vraiment logique.
Il y a donc cette satanée primitive qui me soucie.

Le dessin est resté calé quelque part.


----

Il faut évidemment remplacer les quelques y que j'ai écrit par des z dans mon message précédent.

Poser x=z.t (z est ici une constante puisque x est la variable d'intégration)

dx = z.dt
x²+z² = x² + x²/t² = x²(t²+1)/t² = z².(t²+1)
(x²+z²)^(3/2) = z³ . (t²+1)^(3/2)

dx/(x²+z²)^(3/2) = z/[z³ . (t²+1)^(3/2)] dt = (1/z²) . dt/(t²+1)^(3/2)



Poser t = tg(u)
dt = du/cos²(u)

1+t² = 1 + tg²(u) = 1/cos²(u)
(1+t²)^(3/2) = 1/cos³(u)

dt/(1+t²)^(3/2) = du/cos²(u) . cos³(u) = cos(u) du

S dt/(1+t²)^(3/2) = S cos(u) du = sin(u) = sin(arctg(t)) = t/V(t²+1)

Et donc :




-----
Sauf distraction.  

Bonjour à tous,

Je passe en coup de vent.....

JP, votre résultat d'intégrale sur dx avec du x dans le résultat me semble louche. Auriez-vous oublié de remplacer la variable muette par sa valeur ?

Sinon, j'allais proposer un approche semblable à celle-ci : , qui de plus a l'avantage de retomber sur la formule du champ produit par un fil de longueur infini lorsqu'on fait rendre la longueur du segment vers l'infini. Ce dont je ne suis pas sur avec votre formule, mais c'est dur de vérifier.

Je trouve E(M) = 2/(4Pi.€o).Lambda * L/(z.V(L²+z²))

Si le fil était infiniment long on aurait L > > > z et donc V(L²+z²) pratiquement = L

et le champ en M tendrait alors vers : E(M) = 2/(4Pi.€o).Lambda * L/(z.L) = 2/(4Pi.€o) . Lambda/z (avec z la distance entre M et le fil).

Et E = 2/(4Pi.€o) . Lambda/z est bien le champ produit en un point de l'espace distant de z d'un fil infini rectiligne uniformément chargé de densité linéique de charge Lambda.

Non ?

alban,

En plus de ma réponse précédente.

Je n'ai pas du "x" dans le résultat de mon intégrale mais uniquement dans une primitive permettant de calculer l'intégrale.

Comme indiqué avant ( 23-11-11 à 10:20) le résultat que j'ai trouvé est :

E(M) = 2/(4Pi.€o).Lambda * L/(z.V(L²+z²))

Merci beaucoup J-P,
Mais j'ai décroché à partir du moment où l'on pose t=tg(u)
J'ai compris la 1^ère partie de l'intégration mais le reste...
Je pense que j'essaie de faire des choses qui ne sont pas de mon niveau (je prépare un concours niveau post-bac, 1^ère année de prépa)
Je me résigne donc à admettre le résultat à partir de ce point là...
En tous cas un grand merci à vous deux et bonne soirée.
C'est grâce à des passionnés comme vous que des curieux comme moi gardent l'envie d'apprendre.
Continuez ainsi et surtout ne changez rien, a +