Niveau autre

Sédimentation

Posté par
Kiecane 17-04-19 à 18:52

Bonsoir,

J'ai un problème avec l'exercice suivant :
On étudie une particule sphérique de rayon R, de masse volumique dans un bécher rempli d'un liquide de masse volumique '< et de viscosité . La particule est soumise à son poids, à la poussée d'Archimède et à une force de frottement $\vec{f}=-h\vec{v}$ . Le mouvement de cette particule est rectiligne descendant.
On note (Oz) l'axe vertical ascendant et g la norme du champ de pesanteur terrestre. On exprimera le résultat avec m*=(1-('/))m

Voici ce que j'ai fait (je ne détaille pas toutes les étapes):
J'ai exprimé toutes les forces en fonction de $\vec{u_{z}}$
$\vec{f}=hv\vec{u_{z}}$
$\vec{\prod{}}=\frac{4}{3}\pi R^{3}\mu 'g\vec{u_{z}}$
$\vec{P}=-\frac{4}{3}\pi R^{3}\mu g\vec{u_{z}}$

Ensuite j'ai appliqué la seconde loi de Newton :
$\vec{f}+\vec{P}+\vec{\prod{}}=m\vec{a}$
$hv+\frac{4}{3}\pi R^{3}\mu 'g-\frac{4}{3}\pi R^{3}\mu g=-m\frac{dv}{dt} \\$ (j'ai mis un signe - car la vitesse diminue quand z augmente)
Et je trouve en développant : $\frac{dv}{dt}+\frac{h}{m}v=(1-\frac{\mu '}{\mu })g=\frac{m*}{m}g$
Mais dans la correction il y a écrit qu'on doit trouver : $\frac{dv}{dt}+\frac{h}{m}v=-\frac{m*}{m}g$ et je ne vois pas pourquoi on aurait un moins.....
Je me suis rererererelue et je ne vois vraiment pas où est mon erreur.

Merci d'avance pour votre aide !

Posté par re : Sédimentation 17-04-19 à 22:56

Bonsoir
Je ne sais pas si l'orientation choisi de l'axe (Oz) vient de toi ou est imposée par l'énoncé. Quoi qu'il en soit : orienter l'axe vers le haut alors que l'intégralité du mouvement s'effectue vers le bas : franchement ... du pur masochisme.
Enfin, en conservant un axe vertical ascendant, on peut écrire :

$\overrightarrow{f}=-h.\overrightarrow{v}=-hv\vec{u_{z}}\quad\text{(avec \ensuremath{v<0})}$

$\overrightarrow{\prod}=\frac{4}{3}\pi R^{3}\mu'g\vec{u_{z}}=\frac{\mu'}{\mu}.m.g.\overrightarrow{u_{z}}\quad;\quad\vec{P}=-\frac{4}{3}\pi R^{3}\mu g\vec{u_{z}}=-m.g.\overrightarrow{u_{z}}$

$\overrightarrow{a}=\frac{d\left(v.\overrightarrow{u_{z}}\right)}{dt}=\frac{dv}{dt}.\overrightarrow{u_{z}}\quad;\quad\text{(avec \ensuremath{\frac{dv}{dt}<0)}}$

En projetant la RFD sur l'axe :

$\\ m.\frac{dv}{dt}+h.v=\left(\frac{\mu'}{\mu}-1\right).m.g$
Cela conduit à l'équation différentielle de ton corrigé.

Posté par re : Sédimentation 25-04-19 à 15:58

Bonjour,

Non ce n'est pas moi qui est choisi cet orientation de l'axe En fait je pense que ce qui me pose problème c'est que je pensais (mais j'imagine que c'est faux) qu'une force devait toujours s'écrire $\vec{F}=\parallel\vec{F}\parallel \vec{u_{x}}$ (j'ai mis x mais bien sûr ça peut-être n'importe quel axe) avec $\parallel\vec{F}\parallel>0$ par définition d'une norme. Du coup vu qu'on avait la vitesse qui diminuait quand z augmente je me disais qu'en mettant un signe - devant dv/dt on avait bien quelque chose de la forme $\vec{F}=\parallel\vec{F}\parallel \vec{u_{x}}$ avec -dv/dt>0. Est-ce que tu pourrais éclaircir tout ça stp ?

En plus dans un autre exercice (cf ci-dessous) on avait fait quelque chose comme ça :
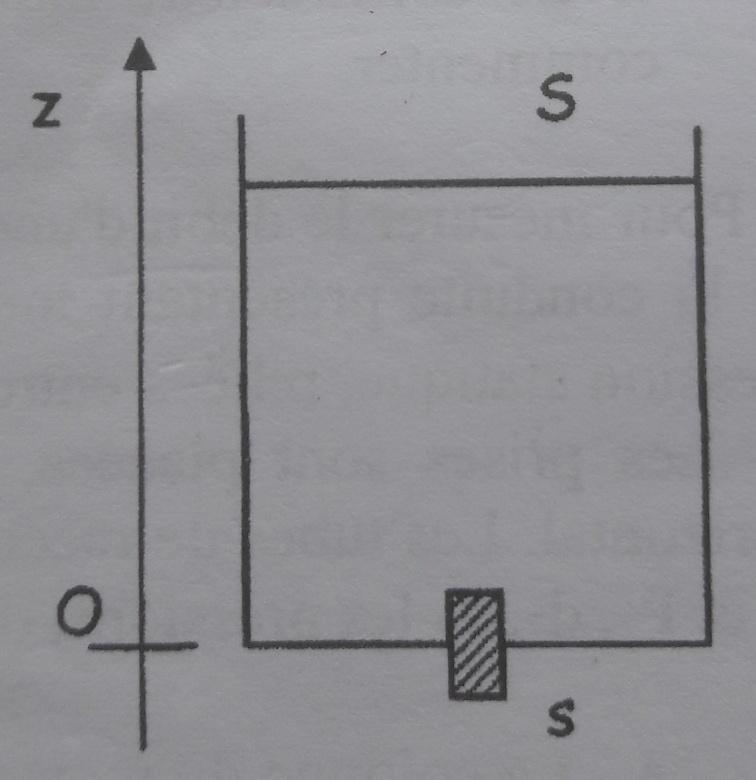
Un récipient de section S est rempli jusqu'à la hauteur H d'eau (considérée comme un fluide non visqueux incompressible). Le fond du récipient est percé d'un orifice de faible section s (s négligeable devant S). A l'instant t=0 où commence la vidange, la hauteur d'eau dans le récipient est égale à H et à un instant t elle devient z. L'écoulement est supposé quasi-permanent. Trouver l'équation différentielle donnant la hauteur d'eau en fonction du temps.
On avait établi : $\sqrt{2gz}\frac{s}{S}=v(z)$ et on avait dit que $\frac{dz}{dt}<0$ car z diminuait quand t augmentait. Donc si on voulait une grandeur de vitesse positive on devait mettre un signe - : $\sqrt{2gz}\frac{s}{S}=-\frac{dz}{dt}$
Du coup je suis un peu perdue... Pourquoi ici il faut mettre un - et dans le cas précédent il ne faut pas ?

Sédimentation

Posté par re : Sédimentation 25-04-19 à 18:28

Pour un vecteur quelconque, on écrit :

$\vec{F}=\parallel\vec{F}\parallel\vec{u_{x}}$ si le vecteur force a même direction et même sens que le vecteur unitaire. On écrit :

$\vec{F}=-\parallel\vec{F}\parallel\vec{u_{x}}$ si le vecteur force est de même direction et de sens opposé au vecteur unitaire. Le problème se complique lorsqu'on n'utilise pas la norme du vecteur mais seulement la lettre F ou v. Il y a alors ambiguïté. Dans certains problème F désigne la norme du vecteur, il faut donc appliquer les règles précédentes, dans d'autres problèmes, F désigne la mesure algébrique qui est soit positive soit négative selon le sens du vecteur. Pour lever cette ambiguïté tout en allégeant l'écriture, on peut aussi convenir de noter F pour la norme et F_x pour la composante du vecteur sur l'axe (valeur algébrique).

Dans l'exercice sur la vidange du réservoir, v(z) désigne la norme du vecteur. Il aurait été plus clair de noter :

$\frac{s}{S}\sqrt{2g.z}=\Vert\overrightarrow{v_{(z)}}\Vert=-\frac{dz}{dt}$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Sédimentation

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique