Bonjour, j'aurai besoin d'aide pour que vous me dites si ce que j'ai fais est correcte ou pas.

J'ai seulement le sujet de tête, car le site où se trouve actuellement le sujet rencontre quelques problèmes...

Une roue sur une route horizontal arrive au temps T₀= 0 sur sur une route sinusoïdale.

On néglige les frottements et le rayon de la roue, sur cette roue se trouve une masse rectangulaire m, un ressort de longueur nulle au repos et un dispositif qui tient le tout parfaitement vertical et on négligera ce dernier dispositif...

Durant toute l'expérience, la roue va à une vitesse constante V_x.



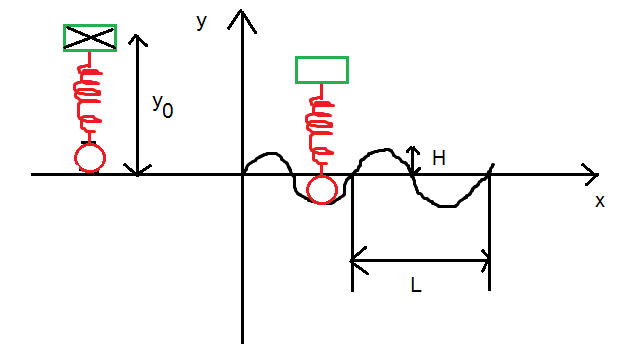
1)Déterminer l'équation du mouvement du point de contact entre la roue et le sol.

x(t) = V_xt

y(t) = H sin(2/L x) = H sin(2/L V_xt)


2) Appliquer le PFD sur l'axe y et en déduire une équation différentiel.

F : Force du ressort sur la masse m

R - P + F = m y" = > y" + k/m y = 0


3) Résoudre cette équation différentiel.

y'(t) = -k/m ₀^t y(t) dt

= -k/m  ₀^t  H sin(2/L V_xt) dt

= kHL/2V_xm cos(2/L V_xt)


y(t) =  kH²L² / 4² V_x²m sin(2/L V_xt) + y₀


4) Trouver la vitesse pour un confort maximal de la voiture sachant que la période T_max est la période maximal de confort (dès que j'aurai accès au sujet je le mettrai car là, les questions sont un peu vague...)

y(t) =  kH²L² / 4² V_x²m sin(2/L V_xt) + y₀


La fonction y(t) possède une période T = 2 / (2V_x/L) = L/V_x

Pour T_max :

V_max = L/T_max

Fin.

Merci d'avance.