Inscription / Connexion Nouveau Sujet
Rétroprojecteur/optique
Bonjour,
On désire projeter l'image de AB(sur feuille transparente) sur un écran placé à une distance D de l'axe optique de la lentille (L).
L'ensemble lentille-miroir du rétroprojecteur est réglable en hauteur. Le miroir plan est incliné de 45° ,la lentille a une vergence de V=1/f'=2,0 dioptries et la distance lentille-miroir (fixe) est d=10 cm
AB est placé à une distance telle que h>f'
On représente (pour le point A) l'ensemble des transformations pour le diagramme:
A->A'-> A'' L et M sont placés au dessus de chaque flèche et ils désignent respectivement la lentille et le miroir.
Dans cette configuration on a : OA>OS où S est le centre du miroir.
Les distances h,D et d sont définies comme positives.
1.1 déterminer la distance objet-lentille h permettant d'obtenir une image nette sur l'écran. On exprimera h en fonction de D ,d et V
1.2 En déduire que la distance minimale de D est Dmin=f'-d
1.3Donner le sens de variation de la fonction h(D) pour D>Min
1.4En déduire s'il faut abaisser ou monter l'ensemble L-M quand on éloigne le rétroprojecteur de l'écran.
1.5 définir et déterminer le grandissement (en valeur absolue) total en fonction de D,d et V. AN pour D=3m
je bloque dès la question 1. Pouvez vous me donner une piste pour débuter svp ? merci d'avance.
Bonjour
Tu as intérêt bien sûr à faire un schéma soigné avec la marche de quelques rayons lumineux.
Méthode :
Construire l'image A1B1 de AB par la lentilles convergente. Les formules de conjugaisons de Descartes devraient te permettre de quantifier précisément ce que tu obtiens graphiquement.
Construire l'image définitive A'B' sur l'écran en considérant que A'B' est le symétrique de A1B1 par rapport au plan du miroir.
Remarque : graphiquement, il est peut-être plus pratique de procéder en sens inverse : placer A'B' sur l'écran ; déterminer A1B1 comme le symétrique de A'B' par rapport au plan du miroir ; placer AB de sorte que l'image de AB par la lentille soit A1B1...
Je te laisse réfléchir à tout cela...
Hello à tous les 2
J'espère que Vanoise ne m'en voudra pas d'exhiber le beau dessin pour lequel je viens de passer 20 minutes en tirant la langue .. 
En espérant que cela mettra Openmind2205 sur le bon chemin optique
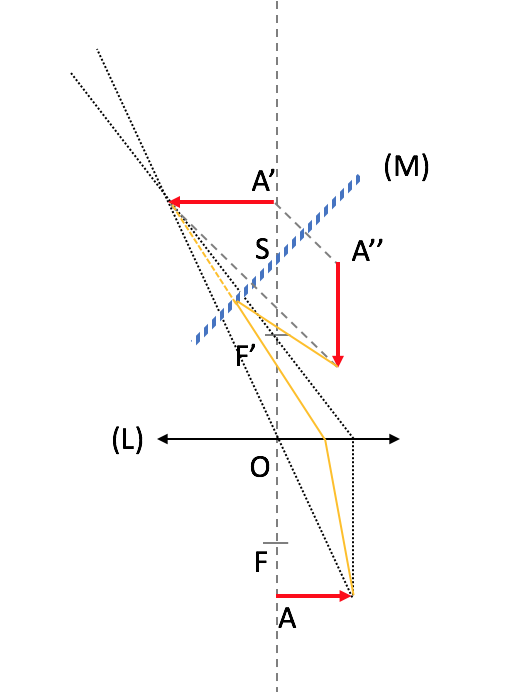
Merci beaucoup pour vos réponses 
Alors pour la 1) :
D'après la relation de conjugaison j'ai pu déterminer h qui est égale à
2) Si h tend vers l'infini alors D devient minimale on a alors:
(d+Dmin)- 1/v=0 (<=> h tend vers l'infini)
<=>d+Dmin- f'=0 <=> Dmin= f'-d
3) Dois-je dériver par rapport à D ?
h(D) =
h'(D)=
Donc quelques soit la valeur de D , le sens de variation de D pour D>Dmin est strictement décroissante est bon
Bonjour
Tout à fait d'accord avec ton dernier message. On pouvait aussi arriver au même résultat sans faire de calcul de dérivée. Il suffisait de raisonner sur la formule de conjugaison de Descartes :
Pour avoir D minimum, il faut avoir : maximum. Cette valeur maximale de
est obtenue pour (1/h) minimum soit (1/h)=0. En pratique évidemment, il n'est pas possible de faire tendre h vers l'infini.
Directement :
Plus généralement, la première relation que j'ai écrite montre bien que si h augmente D diminue.
Je te laisse terminer...
Merci beaucoup de votre explication 
pour la question 1.4 : j'ai dit que si on augmente D pour avoir une image nette il faut abaisser le système pour diminuer h


