Niveau maths sup

Résultantes des forces de Lapalce sur un cadre champ non uniform

Posté par
Lupa99 27-10-18 à 23:04

Bonjour,

Dans un système de coordonnées cartésiennes, on considère un champ $\vec{B} = B(x)\vec{u_y}$ .

Un cadre rectangulaire parcouru par un courant permanent I est positionné de la façon suivante :

- Deux de ses côtés sont parallèles à l'axe (Ox).
- Le vecteur $\vec{u_y}$ est perpendiculaire au cadre.

Calculer la résulante des forces de Laplace.

Je n'arrive pas à gérer comme il faut les orientations du courant... car à chaque fois que je fais le calcul, je n'arrive pas à montrer que la résultante des force de Laplace d'un des côté parallèle à (Ox) est l'opposé de celle de l'autre côté parralèle.

Voici mon calcul :

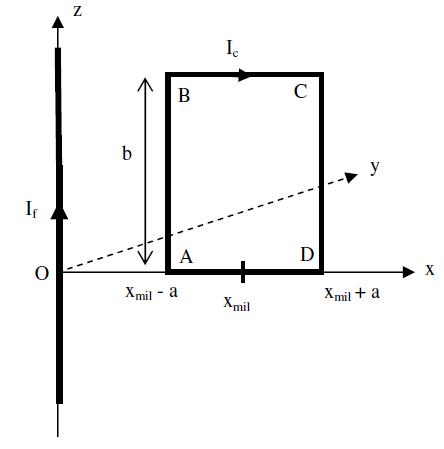
(J'ai repris un schéma d'un autre post pour que ce soit plus clair, il faut cepandant ne pas prendre compte de l'axe (Oz) et du fil, et considérer B // un certain uy perpendiculaire au plan du dessin)

-J'oriente le contour (donc les "dl") dans le sens du courant.
-J'ai sur le segment BC , $\vec{dl} = (+\vec{u_x}dx)$ , sur DA : $\vec{dl} = (-\vec{u_x}dx)$
- J'ai donc : $\int_B^CI\vec{dl}\wedge\vec B = I\int_{x-a}^{x+a} B(x)dx \vec{u_x}$
- J'ai donc : $\int_D^AI\vec{dl}\wedge\vec B = I\int_{x+a}^{x-a} -B(x)dx \vec{u_x} = = I\int_{x-a}^{x+a} B(x)dx \vec{u_x}$
Et donc l'égalité des deux intégrales... (J'intègre sur le chemin A-B-C-D-A pour avoir la résultante des forces de Laplaces).

Où est mon erreur de raisonnement ?

Je vous remercie par avance !

Résultantes des forces de Lapalce sur un cadre champ non uniform

Posté par re : Résultantes des forces de Lapalce sur un cadre champ non un 27-10-18 à 23:36

Bonsoir
Le plus simple consiste à t'intéresser à la force élémentaire dF exercée sur la portion élémentaire de longueur dl centrée en x (x compris entre x_m-a et x_m+a) de fil du coté AD et à comparer à la force élémentaire dF' exercée sur la portion élémentaire de même longueur dl, centrée également en x mais appartenant au côté BC. Puisque le champ magnétique ne dépend que de x, il a même vecteur B au niveau des deux éléments de fils. Les deux éléments de fils ont même longueur, sont parallèles et sont parcourus par des courants de même intensité mais de sens inverse. Ces deux forces élémentaires sont donc opposées. Le raisonnement étant valide quel que soit x compris entre x_m-a et x_m+a, les deux forces sont opposées. Ce raisonnement est plus simple que le tien et présente l'avantage de pouvoir aussi, si cela est demandé plus loin dans le problème, s'appliquer au moment des forces. Si tu veux des formules :

$\overrightarrow{dF}=I.\overrightarrow{dl}\wedge\overrightarrow{B}\quad;\quad\overrightarrow{dF'}=I.\overrightarrow{dl'}\wedge\overrightarrow{B'}$

$\overrightarrow{dl}=-\overrightarrow{dl'}\quad;\quad\overrightarrow{B}=\overrightarrow{B'}$

donc :

$\overrightarrow{dF}=-\overrightarrow{dF'}\;\forall x\in[x_{m}-a,x_{m}+a]$

Dans ton calcul, il ne faut pas à la fois inverser le sens de circulation et remplacer dx par (-dx). Le produit vectoriel est colinéaire à $\overrightarrow{u_{z}}$ .

Posté par re : Résultantes des forces de Lapalce sur un cadre champ non un 28-10-18 à 09:08

Merci pour votre réponse !
J'aime bien cette façon de voir, je vais bien la mémoriser, c'est beaucoup plus intuitif !

Cependant, j'aimerais quand même savoir pourquoi inverser le sens de circulation était une erreur ?
(Oui d'ailleurs, c'était pas ux mais bien uz le vecteur directeur du produit vectoriel, mais passons...)

J'explique mon raisonnement erroné a priori : j'ai remplacé dans l'intégrale la valeur de $vec {dl}= -dx vec u_x$ . Jusqu'ici normalement j'ai le droit non ? Et cela n'inverse pas à priori les bornes, si ? J'ai donc inversé le sens de circulation avec le "-", comme si c'était une intégrale sur un segment en maths.
Mon erreur de signe ne serait pas le fait d'avoir sorti le I de l'intégrale ? (Pourtant, j'ai choisi l'orientation du circuit de même sens que I, donc en factorisant par I je devrais pas avoir de changement de signe, si ?) Le signe de I est-il bien positif tout le long du circuit ?

En bref, pouvez vous m'expliquer un peu plus en détail mon erreur mathématique s'il vous plaît ? J'ai à cœur de corriger mes erreurs de raisonnement pour ne pas les réappliquer dans une autre situation

Posté par re : Résultantes des forces de Lapalce sur un cadre champ non un 28-10-18 à 11:52

L'erreur que tu as commise concerne les bornes d'intégration. Elle est d'ailleurs assez fréquente. Tu as peut-être rencontré cette difficulté pour déterminer des vecteurs champ électrique ou magnétique par intégration de la loi de coulomb ou de la loi de Biot et Savart.
Concrètement ici pour le côté AD : compte tenu du sens du courant, en considérant I>0, tu as :

$\overrightarrow{dl}=-\Vert\overrightarrow{dl}\Vert.\overrightarrow{u_{x}}$

Si tu poses : $\Vert\overrightarrow{dl}\Vert=dx$ comme tu le fais, tu considères la variation élémentaire de x positive : dx>0. Tu dois donc intégrer de la valeur de x la plus faible à la valeur de x la plus forte : de x_A à x_D.

Posté par re : Résultantes des forces de Lapalce sur un cadre champ non un 29-10-18 à 11:37

Super ! Miles mercis, j'ai tout compris maintenant

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Résultantes des forces de Lapalce sur un cadre champ non uniform

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique