Inscription / Connexion Nouveau Sujet
résultante R et le point d?application de
voila Monsieur gbm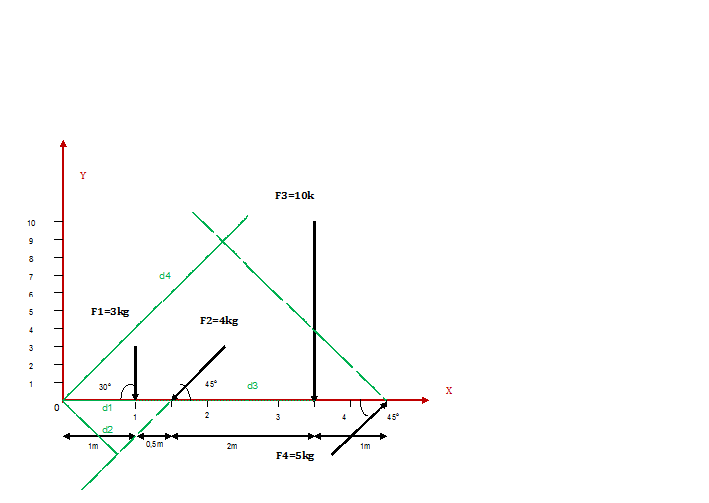
***Forum changé***
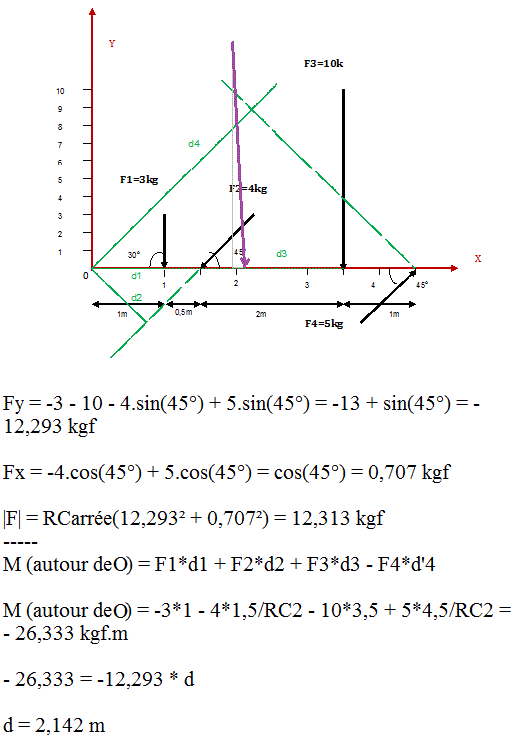
d1 = 1,00 m
d2 = 1,5xsin45 = 1,06 m
d3 = 1+0,5+2 = 3,50 m
d4 = 4,5xsin45 = 3,18 m
Calculons la résultante R
Ry = -3 - 4x0,709 - 10 +5x0,643 = 12,621 kgf
Rx = 0- 4x0,707 + 0 + 5x0,766 = 1,002 kgf
R= Rx2 + Ry2 = (12,621)2 + (1,002)2
= (12,621)2 + (1,002)2 R = 12,66 kgf
R = 12,66 kgf
Déterminons le point d'application de la résultante
∑M F/o = 3x1,00 + 4x1,06 + 10x3,5 - 5x3,18
∑M F/o =3+11,2+35+15.9=33.30 kgf
M R/o = M Rx/o + M Ry/o
Donc : M Rx/o + M Ry/o = 33.30
Rx(0) + Ry(dRy) =33.30 kgf
dRy = 33.30 kgf/Ry = 33.30/12,26
dRy = 2,64m
Si on veut déterminer la direction de la résultante R, on
cherche l'angle α
tg(α) = Ry/Rx  α
α
Cela ne me paraît pas très cohérent.
Par exemples :
- Pour F4, il est indiqué 45° sur le dessin ...
Mais tu utilises un autre angle pour calculer Ry et Rx
- Pour F1, sur le dessin, il est indiqué un angle de 30° manifestement faux (dessiné à 90°)
Essaie donc de donner un énoncé sans ambiguïté et propose tes calculs en concordance avec cet énoncé.
Sauf distraction. 
RX=-4(cos45)+5(cos45)=1(cos45)=0.707 kgf
Ry=3+4(cos45)+10-5(cos45)=13-0.707=12.293 kgf
R= Rx2 + Ry2 
= (0.707)2 + (12.293)2 
=12.313
c'est juste?
RX=-4(cos45)+5(cos45)=1(cos45)=0.707 kgf
Ry=3+4(cos45)+10-5(cos45)=13-0.707=12.293 kgf
R= Rx2 + Ry2

= (0.707)2 + (12.293)2

=12.313
c'est juste?
Il manque l'unité.
Et les racines carrées sont mal écrites, mais soit.
Attention aussi aux signes de Rx et Ry qui sont imposés puisque les axes du repères sont donnés.
Reste à calculer le moment résultant (par exemple autour de O) ... pour pouvoir situer le point d'application de R.
Sauf distraction.

Calculons la résultante R
Rx = 4(cos45°)-5(cos45°)= -1(cos45°)
Rx = -0.707 kgf
Ry = 3 + 4(cos45°)+10-5(cos45°)= 13-(cos45°)
Ry = 12,293 kgf
R= RX2+RY2
RX2+RY2
R= (0.7072+(12.293)2
(0.7072+(12.293)2
R = 12,313 kgf
c'est juste?
d1 = 1,00 m
d2 = 1,5xsin45 = 1,06 m
d3 = 1+0,5+2 = 3,50 m
d4 = 4,5xsin45 = 3,18 m
∑M F/o = 3x1,00 + 4x1,06 + 10x3,5 - 5x3,18
M F/o =3+11,2+35+15.9=33.30 kgf
M R/o = M Rx/o + M Ry/o
Donc : M Rx/o + M Ry/o = 33.30
Rx(0) + Ry(dRy) =33.30 kgf
dRy = 33.30 kgf/Ry = 33.30/12,293
dRy = 2,279m
C'est ça jp?
M. jp je peux exposer un autre problème ici ?
Non, règle du site : 1 seul exercice par topic.
Ouvre un nouveau sujet.


 =900
=900