Inscription / Connexion Nouveau Sujet
Résultante des actions sur liaison pivot
Bonjour,
Voici l'énoncé de l'exercice où je suis bloqué : (j'ai joint un schéma pour aider)
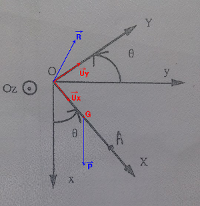
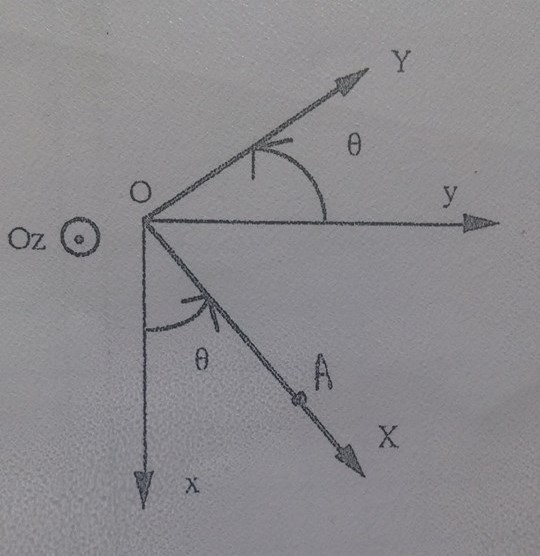
Une tige homogène OA, de masse m, de longueur L, peut tourner sans frottements autour de l'axe fixe horizontal Oz. La position de la tige est repérée par l'angle a entre les axes Ox et OX. On note R (vecteur) la résultante des actions exercées en O par l'axe de rotation Oz sur la tige.
Déterminez les composantes Rx et Ry de cette force suivant les axes tournants OX et OY.
Je suis vraiment bloqué car je ne sais pas par où commencer ! Les moments de nous aident pas car le moment de cette force par rapport à Oz est nul et je ne vois pas comment on peut utiliser le PFD sur une tige...
Merci d'avance pour votre aide !
Bonjour
Commence par déterminer le mouvement de la tige OA par application du théorème du moment dynamique (ou théorème du moment cinétique) ou en raisonnant sur la conservation de l'énergie mécanique. Tu en déduiras les caractéristiques du vecteur accélération du centre d'inertie G de la tige. La relation fondamentale de la dynamique te fournira ensuite les caractéristiques de la réaction de l'axe...
Je te laisse réfléchir un proposer une solution...
Merci de votre réponse.
Pour l'accélération de G c'est fait mais je ne vois pas le rapport entre la force en O et l'accélération du point G...
Si tu choisis comme système, la tige homogène(OA) de masse m, de longueur L, de centre d'inertie G, comme repère, le repère (O,x,y,z) lié à la terre et considéré comme galiléen, les lois de la mécanique t'ont permis d'obtenir les expressions de la vitesse angulaire et de l'accélération angulaire
en fonction de
, des caractéristiques de la tiges, de g et des conditions initiales...
En décomposant l'accélération de G en composante normale et composante tangentielle, on obtient :
La RFD (théorème du centre d'inertie si tu préfères) conduit à :
En exprimant le vecteur poids dans la base mobile tu vas aboutir aux expressions de RX et RY...
Je te laisse réfléchir un proposer une solution... Voici ton schéma complété en tenant compte de mes notations.