On ne voit pas grand chose sur le schéma. Tu peux essayer de le poster à nouveau? A défaut, une (bonne) description du système devrait faire l'affaire.

A oui désolé, je m'étais trompé de lien, voici le bon:



Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Euh... et ça représente quoi exactement? Une petite explication serait la bienvenue.

Tu peux effectivement passer par le calcul de l'énergie potentielle élastique et la dériver par rapport aux coordonnées spatiales pour obtenir l'expression de la force exercée par les ressorts.

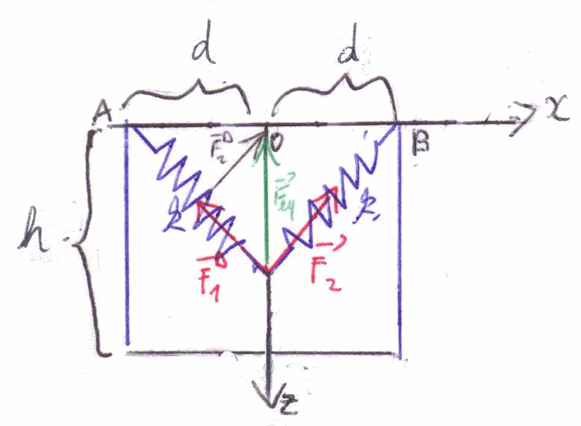
1)Ca représente une nacelle d'un manège modélisée par deux ressorts de chaque côté
2)J'ai dérivée l'Epe et tout, mais je vois pas comment comment calculer la norme de la résultante. Dois je faire un produit scalaire, utiliser pythagore, introduire un angle theta,... Je vois pas du totu comment faire vu que je n'ai pas beaucoup d'infos en plus. Si c'est une de ses méthodes pourrait tu m'expliquer comme l'utiliser stp si c'est une autre pourrais tu m'expliquer aussi?^^

Ça ne suffit pas vraiment comme information.

Le point de contact entre les deux ressorts est-il contraint à se déplacer sur l'axe (Oz)?

Si c'est le cas, on a l'énergie potentielle élastique .

Et l'on a donc, en reprenant la notation de ton schéma,  .

Si c'est ce que tu as calculé, je ne vois pas où est ton problème.


Une autre méthode consisterait à calculer directement et . Si on introduit l'angle formé par ces vecteurs avec la verticale et la longueur des ressorts, on a par exemple (à vérifier):



or, d'après le schéma et .

D'où



Il ne reste qu'à faire la même chose pour et additionner le résultat avec pour obtenir l'expression de la force résultante.

Oui il ne se déplace que sur l'axe Oz. Donc si je comprends bien, j'ai juste à additionner les Epel et par définition en derivant et en multipliant par (-1) la dérivée de Epel j'ai la force resultante? Ce qui me gène c'est pourquoi en addtionnant les 2 Epel ca me donne la force résultante, alors que les forces sont de sens "contraires"(enfin symétriques) je ne vois pas pourquoi on peut additionner les Epel. De plus les ressorts ont la même constante k donc ca revient à Epel=k(d²+z²).

Et l'Epp je ne la prends pas en compte?

J'ai rien dis pour Epp en fait, autan pour moi.

Les énergies potentielles s'additionnent de la même façon que les forces qui en dérivent.

Si l'on a et , la forces résultante s'écrit:



Et tu peux d'ailleurs vérifier dans cet exercice que lorsque l'on dérive l'énergie potentielle totale, on obtient bien une force résultante dirigée selon l'axe vertical uniquement. Ceci traduit le fait que les composantes horizontales des forces exercées par les ressorts sont compensées par la réaction du dispositif qui contraint le déplacement à s'effectuer selon l'axe (Oz) uniquement. Tout est cohérent.

Finalement, le fait d'additionner des énergies potentielles te heurte uniquement parce que tu visualises en même temps les forces correspondantes. Ce qu'il faut avoir à l'esprit, c'est que les énergies potentielles sont des quantités scalaires mais, même si c'est moins évident, elles contiennent exactement la même information que les forces qui sont, elles, représentées sous forme de vecteur... Lorsqu'on les additionne, on n'oublie donc absolument pas de prendre en compte le fait que les forces sont opposées, symétriques ou autres. Cette information est inclue dans l'expression de l'énergie potentielle, pas d'hésitation à avoir donc.

*incluse