Inscription / Connexion Nouveau Sujet
Ressort vertical à masse
Un ressort sans masse et non chargé pend au plafond: sa longueur est de 20cm. On accroche une masse M à extrèmité inferieure du ressort . On maintient cette masse de la main pour que le ressort reste detendu, puis on ôte brusquement la main. La masse se met à osciller. La position la plus basse de masse pendant son oscillation est de 10 cm en dessous de son point de départ a) Quelle est la fréquence d'oscillations
b) Quelle est la vitesse lorsque la masse se trouve 5cm en dessous de sa position originale de repos
c) Une deuxième masse ce 300gr est ajoutée à la première portant le total de la masse à (M + 300) Lorsque le système oscille, sa fréquence est la moitié de la fréquence obtenue avec la masse M seule. Que vaut M?
d) Quelle est la nouvelle position en équilibre?
Bonsoir
Pour les deux première questions : tu peux raisonner sur la conservation de l'énergie mécanique ; je te laisse proposer une solution.
Tu dois aussi connaître l'expression de la période d'oscillation ou savoir la démontrer, tout dépend du niveau exigé...
Connaissant Lo=20cm et L=10cm, pour L=Lo+x, nous pouvons tirer x, qui sera : x=L-Lo, ce qui nous qui nous donne x=10-20=> x=-10cm or Fr=-kx d'où Fr=-k(-10) ce qui donne Fr=10k ou soit, on garde ceci avec x d'abord : Fr=-kx, on peut établir une relation entre l'élongation x, la Force de rappelle Fr et la masse M,
F=m(d²x/dt²) selon Newton.
md²x/dt²=-kx => (d²t/dt²)+(kx/m)=0. C'est par ici que je me bloque, je ne sais plus continuer pour trouver les solutions demandées, veillez me dépanner svp!
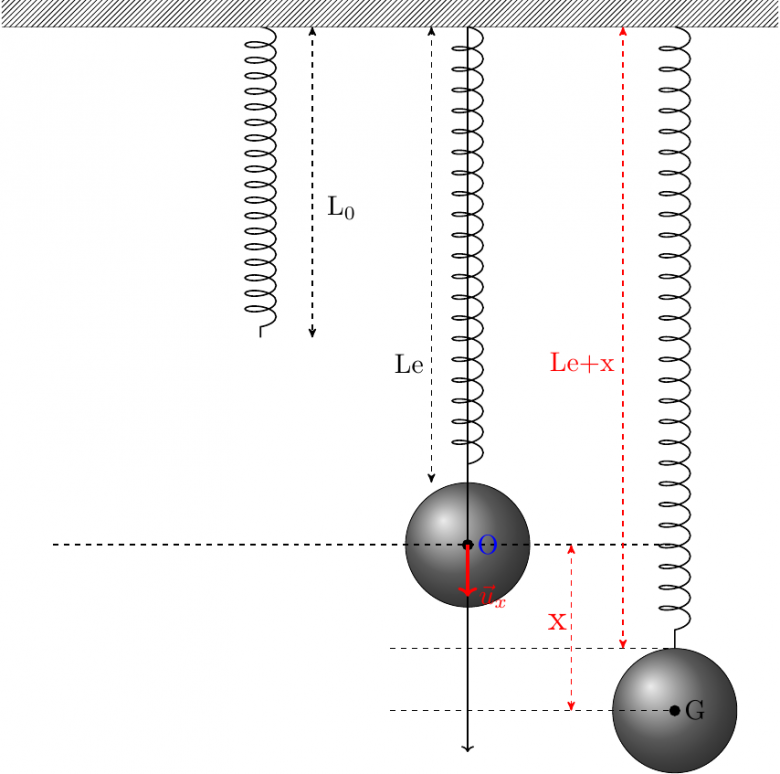
Tu manques un peu de rigueur dans les notations. Pour t'aider un peu, voici un schéma représentant trois situations de gauche à droite.
1° : ressort à vide de longueur Lo ;
2° : ressort avec charge de masse m à l'équilibre : ressort de longueur Le. Il existe une relation simple entre m.g et k(Le-Lo)...
3° : ressort et charge en cours d'oscillations : x désigne l'élongation c'est à dire l'abscisse de G lorsque l'origine du repère est choisi au centre de gravité O de la charge à l'équilibre.
J'imagine que la démonstration de l'équation différentielle du mouvement : (d²t/dt²)+(kx/m)x=0 est demandée. Tu dois savoir qu'une équation différentielle de la forme générale :
(d²t/dt²)+
o2.x=0 admet des solutions de la forme générale :
x=Xm.cos(o.t+
)
Tu doit aussi connaître les relations entre pulsation propre, fréquence et période.
Annuler
connectez vous