Inscription / Connexion Nouveau Sujet
ressort sur plan incliné
bonjour,
voila j'ai un petit probleme tres classique malheureusement je ne sais pas répondre jusqu'au bout...
voila si vous pouvez m'aider merci
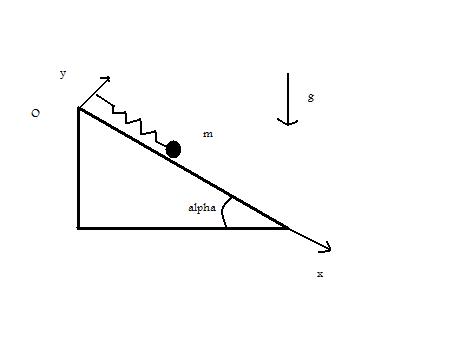
j'ai un ressort de raideur k et de longueur au repos lo dont une extremité est reliée a un point fixe O (en haut du plan) et l'autre extremité est reliée a un point materiel M de masse m (voir le schéma)
voila ma question est :
on cherche la position de la masse M a l'équilibre puis apres avoir déplacé M d'une distance D (suivant l'axe Ox) on lache sans vitesse initiale. trouvez l'aquation régissant l'évolution de x en fonction du temps.
voila ce que j'ai trouvé pour commencer
position de M
OM = x ux + y uy
on est dans un référentiel galiléen avec systeme masse constante
on applique le PFD au systeme masse ressort
somme des forces ?
P+ R + T = ma
il n'y a pas de vitesse sur y on a donc
P+R+T = mdvx/dt
si on projete sur Ox on a :
P = mg sin (alpha)
T = -T ux
R = 0
on a donc
mgsin(alpha) -T ux = mdvx/dt
g sin(alpha) -T/m = dvx/dt
voila ... apres ça je ne sais pas comment faire pour trouver une bonne equation x(t)
il a pas l'air de manquer grand chose
pouvez vous m'aider svp ?
merci
cordialement
akirasilver
Bonsoir,
"R = 0 " ==> R = m g cos
g sin - T/m = d2x / dt2
- T/m = d2x / dt2
Mais T = k x
d2x/dt2 + (k/m) x = g sin
Equation différentielle du second ordre que l'on résout par les méthodes habituelles...
On a un ressort, tu dois être capable d'exprimer l'effort exercé par ce dernier sur la masse de façon plus précise que ça (en faisant notamment intervenir la position de la masse).
Ensuite deux choses:
1. Pose pour en déduire la valeur de x à l'équilibre.
2. Résous l'équation différentielle en obtenue par application du PFD
Oui, R est nulle sur l'axe x mais égale à m g cos sur l'axe y.
sur l'axe y.
La position de la masse à l'équilibre est x0 = l0 + (m g sin /k)
/k)
La solution doit être :
sauf erreur de ma part parce que j'ai fait le calcul sans l'écrire.
Mais cette solution respecte les conditions initiales et semble cohérente avec le problème.
Oui, j'ai oublié l0 si on prend l'origine en O...
Mais je referai le calcul en l'écrivant. Je serai plus sûr de ne pas "en perdre en route"...
a dac merci c'est a peu pres ce que j'ai fini par trouvé ^^
j'ai une autre petite question a propos de l'énergie potentielle de la force exercée par le ressort est ce que c'est une force élastique a 1dimension ? du coup est ce que j'aurai un truc du genre :
integrer -kx ?
et comme c'est une force conservative, ça dépend que des positions initiales et finales ?
et donc on a
F = -k(l-lo)x
or l'énergie potentielle dw=-dU= W de A a B positions initiales
on a donc
F . dx = -dU
-k(l-lo)ux = -dU
or W =  dW =
dW =  -dU
-dU
donc
l'énergie potentielle de la force du ressort est :
1/2 kx² ?
est ce correct ?
merci si vous pouvez m'aider
cordialement
akirasilver
C'est un peu confus...
et comme on a aussi :
et donc
(à une constante près comme toujours évidemment).
L'important c'est que ce n'est pas la position absolue de la masse qui intervient dans l'expression de l'énergie élastique emmagasinée par le ressort, mais l'écart par rapport à la longueur à vide
.
a ouai j'ai pris un cas particulier et c'est pas une bonne idée ...
merci beaucoup pour cette correction
cordialement
akirasilver
bonjour,
je vois que le sujet est vieux mais je tente ma chance quand même.
je bloque sur la question: "trouver l'équation de x en fonction de t lorsque M est déplacé d'une distance D"
c'est sensiblement le même exercice traité ci-dessus mais je ne comprend pas comment vous arrivez à x(t)= x(o)+D cos  (k/m t)
(k/m t)


