Inscription / Connexion Nouveau Sujet
Ressort et plan incliné : dynamique du point
Bonsoir,
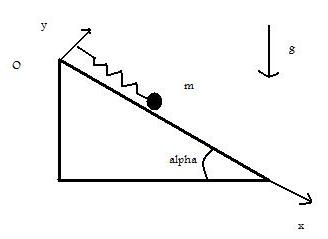
Voilà, cela fait près de 3 jours que moi et mes amis bloquons sur un problème de dynamique du point. Voilà l'énoncé et le schéma :
On considère, sur un plan incliné, un ressort de raideur k et de longueur au repos l0, dont les extrémités sont reliées à un point fixe O et à un point matériel M de masse m. On suppose qu'il n'existe pas de frottement de glissement sur le plan incliné.
La première question nous demande de trouver l'abscisse xe du point M à l'équilibre.
J'ai trouvé : xe=l0+(mgsin
)/k et apparemment c'est la bonne réponse.
La deuxième question : A partir de la position d'équilibre, M est déplacé d'une distance d comptée algébriquement sur Ox et lâché sans vitesse initiale. Etablir l'équation horaire x(t) enfonction de d, k, m et xe.
Donc on applique le PFD : P + F(ressort) = m.a
Au final je trouve a = gsin-((k/m).(xe-l0))
C'est à partir d'ici que nous sommes bloqués.
Nous nous demandons s'il faut intégrer deux fois pour trouver x(t) puisque l'accélération est la dérivée seconde de x.
Ou alors, faut-il poser xe-l0 = x pour tomber sur une équation différentielle ?
Merci d'avance pour votre aide.
Cordialement.
bonsoir,
quand on applique le PFD on tombe forcément sur une équa. diff.
Au final je trouve a = gsin
-((k/m).(xe-l0)) non, ça voudrait dire que a est constante ce qui n'est pas le cas (M oscille)
Donc faut-il poser F(ressort) = -kx dans ce cas là car quand on a P + F(ressort) = m.a il n'y a que F(ressort) qui varie non ?
on ne "pose" pas F = -kx, on applique la définition de la force de rappel:
F = -k
l l étant l'allongement qui vaut ici ....
Oui effectivement merci de la correction.
L'équation différentielle est donc
x''+(k/m)x = g.sin si je ne me trompe pas.
Le problème c'est que par la suite nous trouvons une solution x(t) = cte car g.sin semble constant. Cependant il semblerait que non mais nous ne savons pas pourquoi. Nous pensons que alpha évolue en fonction du temps mais sur le schéma nous ne voyons pas comment. Pouvez vous nous éclairer ?
xe + d c'est la position de départ de M
si un ressort a une longueur à vide de lo,
qu'appelle-t-on allongement du ressort?
Je ne suis pas sûr de ma réponse car cette notion ne me dit rien mais je pense que c'est la différence entre la longueur du ressort et la longueur du ressort à vide. 
Donc l = x - l0 ?
oui, c'est bcp mieux
Je ne suis pas sûr de ma réponse car cette notion ne me dit rien
tu vas quand même pas me dire que tu n'as jamais vu la définition de la force de rappel!
Non justement quand j'ai vu "force de rappel" je suis allé voir sur internet car je n'ai jamais vu ça au lycée.
On a donc F = -k(x-l0) ?
si tu as fais une TS j'ai bcp de mal à te croire.
ceci dit tu devrais maintenant "tomber" sur la bonne équa. diff. 
Avec la réforme j'ai l'impression qu'on a rien vu en mécanique car cette année personne comprend en cours.
J'ai donc x'' + (k/m)x = gsin + (k/m)l0 ?
oui, et comme g sin = k(xe-lo)/m
on trouve finalement:
x" + k/m(x-xe) = 0
on pose: X = x-xe (écart par rapport à la pos. d'éq.)
et on trouve l'éq. tant attendue:
X" + 
o2X = 0
Annuler
connectez vous