Inscription / Connexion Nouveau Sujet
Ressort et frottement solide
Bonjour,
Une fois de plus, je requiert votre aide pour un exercice mélangeant des notions de dynamique et sur l'énergie. Je remercie par avance quiconque acceptant d'user de son temps pour ses problèmes.
Une brique, assimilable à un point matériel de masse m = 1kg, est attachée à l'extrémité d'un ressort idéal de raideur k = 100 N.m-1. Elle glisse sur la table sur laquelle elle repose. Les coefficients de friction statique, μs, et dynamique, μd, entre la brique et la table sont, respectivement, μs = 0,2 et μd = 0,15. La gravitation est considérée de g = 10 m.s−2. La position de la brique à l'équilibre est prise comme référence, x = 0.
1. Montrer que si on lâche la brique sans vitesse initiale d'une position x0,celle-ci ne se met en mouvement que si x0 satisfait une inégalité du type |x0|> x0c où x0c est une distance que l'on précisera en fonction de μs, m, g et k.
2. On place maintenant la brique à x0 = 20cm et on la lâche sans vitesse initiale. En utilisant le théorème de variation de l'énergie totale, montrer que la position x1 sur laquelle la brique s'arrête pour la première fois est donnée par
x1 = (2μdmg)/k − x0
3. La brique repart-elle de la position x1? Si oui, calculer sa position d'arrêt x2.
Pour la question 1. voici ce que j'ai trouvé :
Sachant que μs = F/N avec F force de frottement et N force de réaction du sol,
on a F = μs*N
Or ici, la norme de la force de réaction N est égale à celle du poids P (=mg) soit P = N
Donc : F = μs*N <=> F = μs*P
Avec x0c valeur "limite" où l'égalité est toujours vraie.
Donc F = μs*P <=> k*x0c = μs*P
<=> x0c = (μs*P) / k
<=> x0c = (μs*mg) / k
Par contre pour la seconde question, je bloque. J'ai tenté deux approches, toutes deux sans issues :
Soit Em = Ec + Ep
Avec Em énergie mécanique, Ec énergie cinétique et Ep énergie potentielle.
Donc Em = (1/2)mv² + mgz + (1/2)k(l-l0)²
On cherche la position d'arrivée x1, donc v = 0, donc :
Em(x1) = mgz + (1/2)k(l-l0)²
Soit le théorème de l'énergie mécanique : Em(x1) - Em(x0) =  Epnc
Epnc
Avec x1 position d'arrivée, x0 position de départ, et  Epnc somme de l'ensemble des forces non-conservatrices.
Epnc somme de l'ensemble des forces non-conservatrices.
Puisqu'il n'y a pas de force de frottement dans notre cas, on s'attend à :
Em(x1) - Em(x0) = 0
Soit Em(x1) - Em(x0) = (1/2)kx1² - (1/2)kx0²
<=> (1/2)k(x1² - x0²)
Après quoi je ne sais pas comment obtenir le résultat demandé à l'énoncé.
Pouvez-vous m'aider s'il vous plaît ?
Bonjour
Attention : la conservation de l'énergie mécanique n'est pas vérifiée en présence de frottement.
Pourrais-tu fournir un scan du schéma où serait représentées les différents vecteurs et les différentes notations ?
Il est cependant possible de raisonner sur l'énergie mécanique sachant que, entre deux instants :
 Em=WFNC : travail des forces non conservatives, ici la force de frottement.
Em=WFNC : travail des forces non conservatives, ici la force de frottement.
Non pour la question 2. la force de frottement n'est pas considérée. Désolé je ne sais pas comment vous envoyer un schéma, mais l'ensemble des vecteurs comprend le poids P et la force de réaction du sol N, opposées et perpendiculaire à l'horizontale, et la force de raideur du ressort k. Mon problème étant que je ne sais vraiment pas comment procédé pour obtenir le résultats demandé à l'énoncé. Sans doute, mes deux tentatives sont complètement à côté de ce qu'il faut faire...
Non pour la question 2. la force de frottement n'est pas considérée. Désolé je ne sais pas comment vous envoyer un schéma, mais l'ensemble des vecteurs comprend le poids P et la force de réaction du sol N, opposées et perpendiculaire à l'horizontale, et la force de raideur du ressort k. Mon problème étant que je ne sais vraiment pas comment procédé pour obtenir le résultats demandé à l'énoncé. Sans doute, mes deux tentatives sont complètement à côté de ce qu'il faut faire...
Bonjour
Ilne fait aucun doute que la force de frottement est encore considérée dans la question 2. C'est le thème de ton exercice et c'est pour celà que le coefficient de frottement dynamique µd apparait dans le résultat x1 qu'il faut obtenir.
Utilise l'indication de Vanoise : le TEM (Théorème de l'Energie Mécanique) devra prendre en compte le travail de cette force de frottement (attention au signe, traiter tout mouvement en général me semble très difficile avec un frottement solide : suppose par exemple que x0>0).
Dans ta proposition 2, ton "sigma" n'est pas clair : s'il s'agit d'une somme de forces, ton égalité n'est pas homogène ?... J'ai l'impression qu'en réalité tu écris 2 fois la même méthode, c'est à dire l'emploi du TEM ? Qu'en penses-tu?
Cordialement
Bonjour Nallitsac
Le résultat à obtenir à la question 2, fourni par l'énoncé, fait intervenir le coefficient de friction dynamique. Il faut donc bien tenir compte de la force de frottement. Il suffit d'utiliser le théorème de l'énergie mécanique que je t'ai fourni dans mon message du 08-07-20 à 18:18 entre l'instant initial d'abscisse xo et l'instant final d'abscisse x1. Attention aux signes des abscisses pour calculer le travail de la force de frottement. Pour ne pas te tromper, réalise un schéma propre de la situation. Tu peux éventuellement le scanner et le poster ici.
Bonjour,
Soit F force de frottement : F = μs*mg
Et x0 = x0c = (μs*P) / k
On a : Em(x1) - Em(x0) = F
<=> F = (1/2)mv1² + mgz + (1/2)k(l-l1)² - ( (1/2)mv1² + mgz + (1/2)k(l-l0)² )
<=> F = (1/2)mv1² + mgz + (1/2)k(l-l1)² - (1/2)mv1² - mgz - (1/2)k(l-l0)²
Or, v1 = v0 = 0
Donc : F = mgz + (1/2)k(l-l1)² - mgz - (1/2)k(l-l0)²
<=> F = (1/2)k(l-l1)² - (1/2)k(l-l0)²
<=> F = (1/2)kx1 - (1/2)kx0
<=> F = (1/2)k( x1 - x0 )
<=> 2F = k( x1 - x0 )
<=> 2F/k = x1 - x0
<=> (2μsmg)/k = x1 - x0
<=> (2μsmg)/k + x0 = x1
Et oui, c'était sensé être une soustraction, et non une addition, mais j'ai eu beau retourné l'équation dans tous les sens, c'est le résultat le plus proche de celui attendu que j'ai pu obtenir...
Relis bien mes précédents messages : la variation d'énergie mécanique est égale au travail de la force de frottement, pas à la force.
Bonjour à vous deux
Nallitsac, pour envoyer un schéma (lire la FAQ ![]() [lien] ) qui va te dire :
[lien] ) qui va te dire :
 extrait de
extrait de Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Quelle est l'expression générale du travail d'une force de vecteur fixe pour un déplacement
? Avant tout, il te faut clairement identifier et caractériser les forces appliquées au solide en déplacement ; d'où l'intérêt d'un schéma...
D'accord, donc on a le travail de la force de frottement
WF = //F//.//AB//.cos(180) = -F.AB avec AB = x1 - x0 = 1
Soit WF = -F
Ce qui, si l'on reprend le calcul précédant, donne :
-F*(x1 - x0) = (1/2)k(l-l1)² - (1/2)k(l-l0)²
<=> -F = (1/2)kx1 - (1/2)kx0
<=> -F = (1/2)k( x1 - x0 )
<=> -2F = k( x1 - x0 )
<=> -2F = -k( x1 + x0 )
<=> 2F/k = x1 + x0
<=> (2μsmg)/k = x1 + x0
<=> (2μsmg)/k - x0 = x1
Est-ce correct ?
Cela n'est guère rigoureux...
Rien dans l'énoncé ne permet de poser d'entrée : AB = x1 - x0 = 1 (même pas d'unité !).
Et puis ensuite : mélanger formule littérale et valeur numérique pour en arriver à :
WF = -F ... Cela conduit à penser qu'un travail possède la même dimension physique qu'une force : horreur !!!!
Je note un vecteur unitaire colinéaire à l'axe des x, orienté dans le sens correspondant à un allongement du ressort. L'énoncé précise : xo=20cm. Quand on lâche le solide dans vitesse initiale, la force de rappel exercée par le ressort l'entraîne dans le sens négatif. Le vecteur déplacement, de la position initiale A d'abscisse xo à la position finale B d'abscisse x1 peut donc s'écrire :
La force de frottement est orientée dans le sens opposé au sens du mouvement, donc dans le sens positif. Sa norme vaut µd.m.g (constante de frottement dynamique et non statique). Donc :
Le théorème de l'énergie mécanique, appliqué entre les positions A et B, sachant que l'énergie cinétique est nulle en A et en B, s'écrit :
Je te laisse simplifier ; tu vas obtenir le résultat demandé par l'énoncé... J'imagine que tu as retenu de ton cours de math les identités remarquables, (a2-b2) par exemple...
D'accord, merci pour votre correction.
En effet, j'ai reproduit les calculs depuis les vôtres, je trouve bien le résultat attendu :
WF = F.AB = F.(x1 - x0)
<=> F.(x1 - x0) = (1/2)k(l-l1)² - (1/2)k(l-l0)²
<=> F.(x1 - x0) = (1/2)kx1² - (1/2)kx0²
<=> F.(x1 - x0) = (1/2)k( x1² - x0² )
<=> F.(x1 - x0) = (1/2)k( x1 - x0 ) ( x1 + x0 )
<=> F = (1/2)k( x1 + x0 )
<=> μsmg = (1/2)k( x1 + x0 )
<=> (2μsmg)/k = x1 + x0
<=> x1 = (2μsmg)/k - x0
Très bien ! Ne pas oublier un jour d'examen ou de concours de préciser que la simplification par (x1 - xo) n'est possible que si :
(x1 - xo)  0
0
D'accord, merci. Je tâche donc maintenant de résoudre la troisième et dernière question, mais avant il me faut calculer l'intervalle d'équilibre x0c et la position x1.
A.N. : x0c = (0.2*1*10) / 100 = 0.02 m = 2 cm
On en déduit que la masse reste à l'équilibre si elle est dans l'intervalle [-2 cm, 2 cm].
PS : Pour x1 j'ai fait une erreur de notation, ce n'est pas μs mais μd !
A.N. : x1 = 2 x 0.15 x 1 x 10 / 100 - 0.2 = - 0.17 m = - 17 cm
Donc |x1| = 17 cm
3. Comme |x1| > x0c = 2 cm, on voit que l'équilibre n'est pas réalisé et
que la masse repart donc vers la droite. En appliquant de nouveau le théorème
de l'énergie mécanique on a sur le trajet x1 vers x2, on a :
Vecteur F = -μdmg*(ex) car ici, le vecteur F s'oppose au mouvement vers la droite (contrairement à la question 2 où le mouvement s'effectuer vers la gauche, et où le vecteur de la force de frottement avait le même sens que le vecteur de référence (ex)).
Le vecteur F est toujours constant donc son travail entre x1 et x2 est
WF = -F.(x2-x1) = (-μdmg)(x2-x1)
D'autre part,
Em2 - Em1 = 1/2 k (x2² - x1²)
Donc, le théorème de l'énergie mécanique donne :
Em2 - Em1 = WF
<=> 1/2 k (x2² - x1²) = -(μdmg) (x2-x1)
<=> 1/2 k (x2 + x1) = -μdmg
<=> x2 + x1 = -(2μdmg) / k
<=> x2 = -(2μdmg) / k - x1
AN : x2 = -(2*0.15*1*10) / 100 - (-0.17)
= x2 = -(2*0.15*1*10) / 100 + 0.17
= 0.14 m = 14 cm
Le même raisonnement appliqué aux positions suivantes montre
qu'à chaque fois, la masse va s'arrêter à 3 cm de moins (en valeur
absolue) que la position d'arrêt précédente avec des signes qui alternent.
x0 = 20 cm , x1 = - 17 cm , x2 = 14 cm, x3 = - 11 cm , x4 = 8 cm, x5 = -5 cm, x6 = 2 cm.
Finalement en x6, la masse est dans la zone [-2 cm , 2 cm] et donc s'arrête définitivement.
Tout cela me semble correct ! 
Je ne sais pas si cela est déjà à ton programme, mais si tu as un peu de temps, tu peux faire l'inventaire des propriétés des oscillations dans le cas d'un frottement solide comme ici et dans le cas d'un frottement fluide (force de frottement proportionnelle à la vitesse). Tu devrais obtenir trois différences essentielles. Pour t'aider un peu, voici deux simulations. Par rapport à ton problème, pour que les différences soient plus visibles, j'ai diminué l'importance des frottement de façon à obtenir un nombre plus grand d'oscillations.
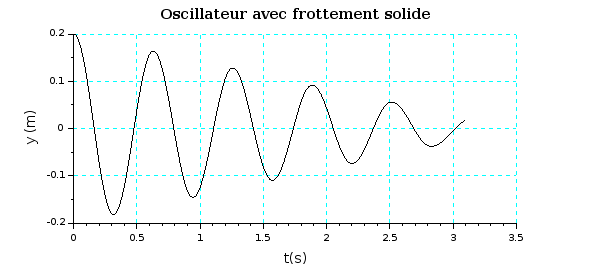
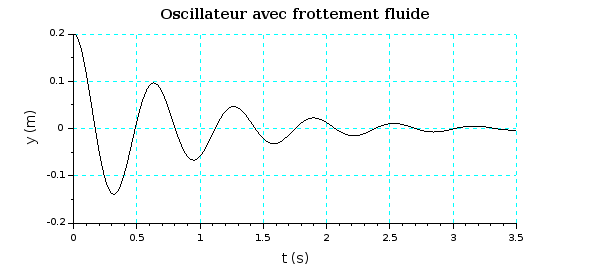
Merci, mais je ne suis pas sur de comprendre à quoi correspond cet inventaire des propriétés d'oscillations.
Tu peux te poser les questions suivantes :
1° Dans chacun des deux cas, comment évolue l'amplitude des oscillations ?
2° Dans chacun des deux cas, que peut-on dire de la position d'immobilisation finale de l'oscillateur ?
Tes connaissances de cours et les réponses à cet exercice devraient te permettre de répondre.
La troisième différence porte sur la valeur de la pseudo-période par rapport à la période propre. Pas sûr que cela soit déjà à ton programme...


