Bonjour,

je suis en L2 Sciences de la vie et j'ai un peu de mal avec cette exercice, et j'aimerai bien avoir un peu d'aide, merci.

Un ressort de masse négligeable, à spires non jointives, parfaitement élastique, est accroché par l'une de ses extrémités à un point fixe. A l'autre extrémité, on accroche un objet de masse
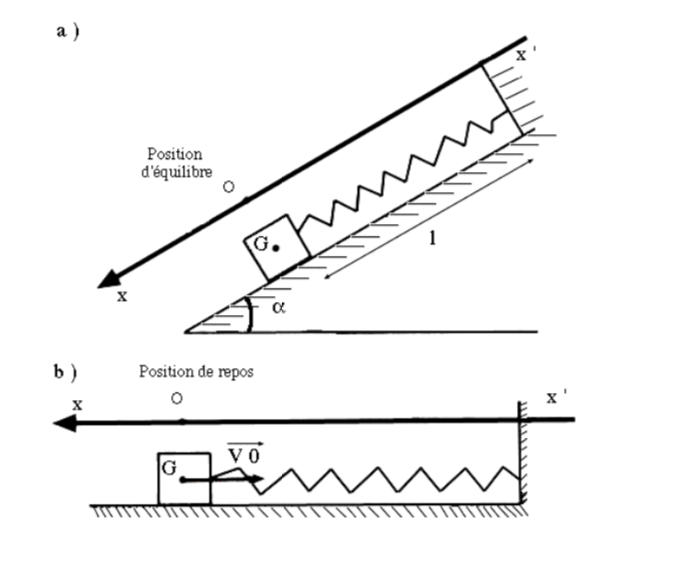
m = 500g. L'ensemble est situé suivant la ligne de plus grande pente d'un plan incliné faisant un angle  = 30° avec l'horizontale. Les frottements sont négligés dans tout l'exercice.
  
a)Le ressort de longueur au repos 10 = 20 cm a, dans les conditions écrites ci-dessus, une longueur 1 = 25
cm à l'équilibre. En déduire la valeur de la raideur k du ressort (on prendra g = 10 m.s-2).
b) On tire l'objet de masse m d'une longueur d = 3 cm vers le bas et on le lâche sans vitesse à l'instant t = 0. Par une étude dynamique, trouver l'équation horaire du mouvement (on choisira l'axe X'X de la figure et l'on prendra comme origine la position d'équilibre de l'objet)
La période des oscillations dépend-elle de  ?

VOIR IMAGE DESSOUS

c) L'ensemble précédent (objet-ressort) est placé horizontalement. L'objet étant au repos, on lui
communique alors une vitesse v0 = - 0,5 m . s-1 à l'instant t = 0 (au cours d'un choc pas exemple).
Etablir l'équation différentielle dans le système d'axe indiqué sur la figure.
En déduire l'équation horaire du mouvement. Autour de quelle position l'objet oscille-t-il ?
d) Comparer la période des oscillations correspondant aux questions b) et c). Conclure.

ce que j'ai fait :
a) je sais que T=-k(x-xo) et w= k/m et si j'isole k =m*wo^2  ou bien k=x-x0/T mais je sais pas la valeur de T ni la valeur de la pulsation ...

b) RFD = P+R+T = ma , ainsi on aura P+R =O mais T=ma, soit -k(x-xo)=ma, donc -kx =m",  donc x"+(k/m)x =O mais après je suis bloqué ...

Merci de votre aide ...