Inscription / Connexion Nouveau Sujet
Ressort avec frottements
Bonjour.
Je n'arrive pas à comprendre le problème suivant :
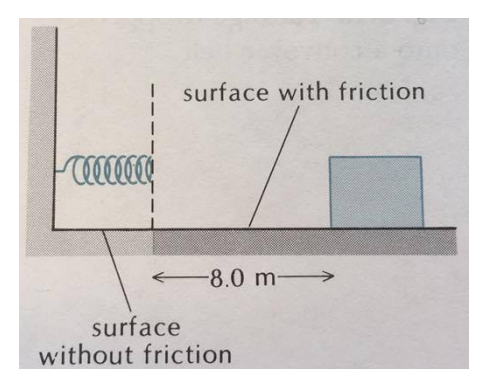
Un ressort se compresse est projette un bloc de 3 kilos sur une surface horizontale.
Pendant que le bloc est collé au ressort, il n'y a pas de frottement. Mais une fois que le bloc s'est détaché du ressort, il y a un frottement de coefficient 0,20.
Le bloc s'arrête à 8m du ressort.
Sachant que la force du ressort est de 120N/m, de combien de mètre le ressort s'est il compressé pour propulser le bloc ?
J'ai essayé de faire 2 schémas, un pendant que le bloc est sur le ressort (il y a trois force, la force du ressort, le poids et la résultante du sol) et après (poids, résultante au sol et la force de frottement)
Puis après j'ai essayé d'appliquer le pfd mais j'ai pas réussi un trouver de réponse.
Bonjour
Phase de contact : raisonner sur la conservation de l'énergie mécanique en absence de frottement. Ensuite : RFD en tenant compte des frottements.
J'ai réalisé deux RDF, un avec le bloc sur le ressort et un autre après que le bloc soit partie.
J'ai donc pour la situation 1 :
ma = -k(l-lo)
Situation 2:
ma = -ud*||N|| = ud*mg (car N = mg) avec ud coefficient de forttement.
Puis en assemblant les deux equations je trouve :
l-lo = (ud*mg)/(-k)
Cependant je n'ai pas utilisé la distance donné donc je pense m'être trompé...
Il faut raisonner sur l'énergie mécanique. Puisque aucune étude de durée n'est demandée, il suffit d'écrire que la variation d'énergie mécanique du système ressort + bloc est égale au travail de la force de frottement. Une fois démontré que la norme du vecteur force de frottement vaut f.m.g ,le problème se résout en une ligne !
Donc si j'ai bien compris, Em = 1/2 *k *(l-lo)² = ud*m*g (avec ud coefficient de frottement)
Ou bien il faut rajouter l'énergie cinétique également ? (dans ce cas, je suis un peu perdu car on a pas la vitesse du bloc)
Théorème de l'énergie cinétique : la variation d'énergie cinétique est égale au travail de toutes les forces : les forces conservatives (FC) et les forces non conservatives (FNC) comme les forces de frottement :
Théorème de l'énergie potentielle : il ne concerne que les forces conservatives :
Théorème de l'énergie mécanique définie comme la somme de l'énergie cinétique et de l'énergie potentielle :
Si tu applique ce dernier théorème à l'ensemble {ressort - bloc} entre l'instant où le ressort comprimé est lâché et l'instant où le bloc s'arrête, tu obtiens :
: le système est immobile à l'état initial et à l'état final ;
avec
: raccourcissement initial du ressort.
Le poids et la réaction normale du support ne travaille pas. Seule travaille la force de frottement d'intensité F, colinéaire au déplacement et orienté en sens inverse du déplacement. Le théorème de l'énergie mécanique conduit ainsi à :
Il te reste à exprimer F...