Niveau maths sup

Ressort

Posté par
ferenc 23-11-11 à 12:15

Bonjour, voici mon énoncé:

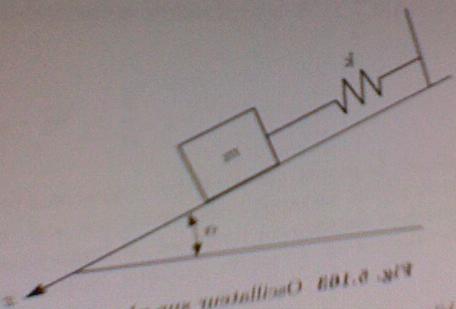
Un point matériel pesant de masse $m$ est astreint à se déplacer sur un droite incliner d'angle $\alpha$ par rapport à l'horizontale. Il se déplace sans frottement. Le point matériel est retenu par un ressort de longueur au repos $L$ et de constante élastique $k$ .

1) Etablir le bilan des forces
2) Trouver l'équation du mouvement et trouver $x(t)$
3) Quelle est la période d'oscillations ?

-------------------------
J'ai un problème à la partie 2:

1) les forces sont évidement $\vec{F}_r$ la force de rappel $\ m\vec{g}$ le poid et $\vec{R}$ la force exercé par la droite sur la masse $m$

2) l'équation est aisément $\ddot{x}=-\frac{k}{m}x+\frac{k}{m}L+g\sin\alpha$ : $(1)$
et la solution de cette équation différentielle est:
$x(t)=A\cos(\omega t+\phi)+B$ , et en dérivant deux fois, on obtient:
$\dot x(t)=-A\omega\sin(\omega t+\phi)$
$\ddot x (t)=-\omega^2x(t)$

$\bullet$ Comme $(1)$ est satisfaite pour tout $t$ , elle l'est aussi pour $t=\frac{\pi-2\phi}{2\omega}$ , ainsi, on obtient $B=-\frac{k}{m}L-g\sin\alpha$

$\bullet$ $(1)$ est aussi satisfaite pour $t=-\frac{\phi}{\omega}$
On obtient ainsi $A(\frac{k}{m}-\omega^2)=0$ et donc $\frac{k}{m}=\omega^2$

Ma question
Une fois arriver là, je ne vois pas comment choisir l'origine des temps pour déterminer $\phi$ , et je ne vois pas comment trouver $A$

merci

Ressort

Posté par re : Ressort 23-11-11 à 20:00

Bonjour,

Il vous manque les conditions initiales.

En fait votre façon de trouver B n'est pa celle que j'utilise. En maths j'ai appris que la solution de ce genre d'équation, avec un second membre qui est ici (k/m)L + g.sin(alpha), est la solution génénrale de l'équaiton homogène (sans second membre) + une solution particuliere de l'équation complète (cette solution est votre B).

Cela étant dit, la résolution de l'équation donne ce que vous avez trouvé, et les constantes indéterminées (constantes d'intégration) sont A et phi. Pour les déterminer il vous faut les conditions initiales ou tout au moins la donnée de la position et de la vitesse de la masse m à un instant donnée. En général on donne position et vitese à t=0. Connaissant cela, vous en déduisez A et phi.

Vu la façon dont la question est posée vous pouvez vous contenter de donner la solution que vous avez trouvée en laissant les deux constantes d'intégration A et phi. Vous pouvez aussi mentionner la façon de les détetminer.

Sinon, pour la pulsation, vous l'avez déjà.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Ressort

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique