Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

résonance avec un ressort

Posté par
cosmoff 11-11-17 à 17:26

Bonjour,

je dois faire un exercice mais le résultat que j'obtiens me parait faux.

Voici l'énoncé :

un ressort est relié à une masse M (sur l'axe des x) posé sur une table (on négligera le poids) et la masse M est excitée (sur l'axe des x) par une force \vec{F_{0}} = F _{0} cos ( \Omega t) \vec{u_{r}}. On négligera les frottements de la table avec la masse M.

déterminer la position de la masse M au cours du temps.

avec le pfd j'ai :

m\ddot{x} = -kx + F _{0} cos ( \Omega t)
résolution de l'équa diff sans second membre :

m\ddot{x} + kx = 0
x(t)= Acos(\sqrt{\frac{k}{m}}t) + Bsin(\sqrt{\frac{k}{m}}t)

solution particuliere: (en utilisant les complexes)
x(t)= \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} cos(\Omega t)

en reliant le tout j'ai :
x(t) = Acos(\sqrt{\frac{k}{m}}t) + Bsin(\sqrt{\frac{k}{m}}t) + \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} cos(\Omega t)

ensuite j'ai déterminé A et B avec les cas particulier ou à x(t=0) = L et la vitesse est nulle à t = 0 :

x(t) = ( L - \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} ) cos(\sqrt{\frac{k}{m}}t) + \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} cos(\Omega t)

Ce qui me pose probleme est que je devrais avoir un x(t) qui varie fortement quand \frac{k}{m} = \Omega ² or moi j'ai la longueur L, alors que c'est la fréquence de résonance et je ne vois pas du tout ou je me suis trompé.

Avez vous une idée de mon probleme ?

Merci d'avance

Posté par
vanoisere : résonance avec un ressort 11-11-17 à 17:36

Bonjour
Tu ne fournis pas une copie intégrale de l'énoncé de l'exercice... Il est probable que celui-ci se contente de l'étude du régime sinusoïdal forcé . Il faut donc se limiter à l'étude d'un régime sinusoïdal de même fréquence que la force d'excitation. Je suppose aussi que x est l'élongation : x(t)=L(t) - Lo
avec L(t) : longueur du ressort à l'équilibre ; Lo : longueur du ressort à vide.
Cela conduit de façon immédiate à :

x(t) =  \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} cos(\Omega t)
L'amplitude tend vers l'infini quand la fréquence d'excitation est égale à la fréquence propre. Bien sûr ce modèle n'est pas réaliste : il faudrait tenir compte des frottements...

Posté par
cosmoffre : résonance avec un ressort 11-11-17 à 18:03

oui j'ai oublié de préciser que  x est bien l'élongation : x(t)=L(t) - Lo.

mon énoncé n'est pas clair car le prof a dit de faire ca chez soi sans trop d'indication (c'était la fin de l'heure), c'est plus un exo pour voir comment on se débrouillerait. Le titre du chapitre est régime sinusoïdal forcé.

le probleme est que mon équation finale n'est pas x(t) =  \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} cos(\Omega t)  maisx(t) = ( L - \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} ) cos(\sqrt{\frac{k}{m}}t) + \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} cos(\Omega t)

De plus ce que tu as mis et le régime permanent du systeme or moi je veux récupérer le régime transitoire et permanent du systeme, or le cheminement de mes équations me donne un résultat faux, as tu une idée de mon erreur ?

Posté par
vanoisere : résonance avec un ressort 11-11-17 à 18:45

Citation :
Le titre du chapitre est régime sinusoïdal forcé

Dans ces conditions, ce que je t'ai indiqué dans mon message précédent est très probablement ce qu'attend ton professeur...
Parler de régime transitoire n'a pas de sens ici puisque les frottements son supposés inexistants (situation totalement irréaliste bien sûr). On peut parler cependant de régime d'oscillations libres qui, dans ce cas limite ne s'amortirait pas... Tu peux donc chercher une solution plus générale de la forme :

x(t) = Acos(\sqrt{\frac{k}{m}}t) + Bsin(\sqrt{\frac{k}{m}}t) + \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} cos(\Omega t)
Pour trouver A et B, il faut connaître l'état du système à t = 0. Par exemple : x(0)=0 ; v(0)=0.
Ceci constitue un "exercice de pensée" intéressant mais ne constitue pas  une modélisation réaliste d'un quelconque dispositif expérimental...

Posté par
cosmoffre : résonance avec un ressort 11-11-17 à 19:10

merci pour tes réponses.

je ne prend pas le cas ou  x(0)=0 ; v(0)=0 car on arrive à 0/0 lorsque \frac{k}{m} = \Omega ²
Si je prend x(0)=L ; v(0)=0 alors j'obtiens :

x(t) = ( L - \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} ) cos(\sqrt{\frac{k}{m}}t) + \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} cos(\Omega t) . Ce qui me pose probleme est que l'oscillation va de L à -L quand \frac{k}{m} = \Omega ² il n'y a donc pas de phénomene de résonance alors que ca devrait...

Posté par
vanoisere : résonance avec un ressort 11-11-17 à 19:29

Tu m'as confirmé dans un message précédent que tu appelles L la longueur du ressort... Il est préférable d'appeler "a" la valeur de (L(0)-L0).
Tu as un problème de calcul de limites : dans le cas limite d'une fréquence d'excitation égale à la fréquence propre, tu obtiens une amplitude qui tend vers l'infini : logique dans la mesure où les frottements sont supposés inexistants :

\lim_{\Omega\rightarrow\sqrt{\frac{k}{m}}}\left(\frac{F_{0}}{m\left(\frac{k}{m}-\Omega^{2}\right)}\right)=\infty
Les conditions initiales que je t'avais proposées conduisent aussi à une amplitude qui tend vers l'infini à la résonance.

Posté par
cosmoffre : résonance avec un ressort 11-11-17 à 19:54

il est la mon probleme, prennons le cas x(0) = 0 et v(0) = 0, on a :

x(t) = \frac{F_{0}}{m(\frac{k}{m} - \Omega ²)} [cos(\Omega t) - cos(\sqrt{\frac{k}{m}}t) ]

donc quand  \frac{k}{m} = \Omega ² nous avons :

x(t) =  \frac{F_{0}}{m(\Omega² - \Omega ²)} [cos(\Omega t)  - cos(\Omega t)]
x(t) = \frac{F_{0}}{m(0)} [0]

nous avons donc x(t) = 0/0, la je coince...

tu m'as donné ensuite le résultat \lim_{\Omega\rightarrow\sqrt{\frac{k}{m}}}\left(\frac{F_{0}}{m\left(\frac{k}{m}-\Omega^{2}\right)}\right)=\infty

mais cette forme me dit que la masse M varie directement entre - Infini et + Infini, il n'y a aucune transition de deplacement. On devrait avoir comme résultat finale une oscillation de plus en plus grande et pas directement une oscillation finale allons de -inf à + inf

Posté par
vanoisere : résonance avec un ressort 11-11-17 à 20:05

Tu ne peux pas espérer un résultat réaliste en négligeant totalement les frottements. Une modélisation fréquente consiste à faire intervenir une force de frottement proportionnelle à la vitesse. Tu tombes alors à une équation différentielle de la forme :

m\ddot{x}=-kx-\alpha.\dot{x}+F_{0}cos(\Omega t)
Le résultat obtenu ainsi est beaucoup plus réaliste !

Posté par
cosmoffre : résonance avec un ressort 11-11-17 à 21:36

oui en prenant en compte les frottements on a une oscillation qui tend petit à petit vers une valeur maximale. Mais c'est bizarre que si on prend pas en compte les frottements on arrive pas a une forme satisfaisante de x(t)

Posté par
vanoisere : résonance avec un ressort 11-11-17 à 23:31

Le problème est donc d'étudier la limite quand \Omega\rightarrow\omega_{0} de :

Y=\frac{\cos\left(\Omega t\right)-\cos\left(\omega_{0}t\right)}{\omega_{0}^{2}-\Omega^{2}}

Un peu de trigo :

Y=2\frac{\sin\left(\frac{\omega o-\Omega}{2}t\right)\cdot\sin\left(\frac{\Omega+\omega o}{2}t\right)}{\left(\omega_{0}-\Omega\right)\left(\omega_{0}+\Omega\right)}

Tu as dû étudier en math :

\lim_{x\rightarrow0}\frac{\sin\left(x\right)}{x}=1 et \lim_{x\rightarrow0}\frac{\sin\left(a.x\right)}{x}=a

Tu peux aussi effectuer un développement limité de Taylor. Quand \Omega\rightarrow\omega_{0}, on peut écrire, au premier ordre près :

Y\approx t\cdot\frac{\sin\left(\omega_{0}t\right)}{2\omega_{0}}

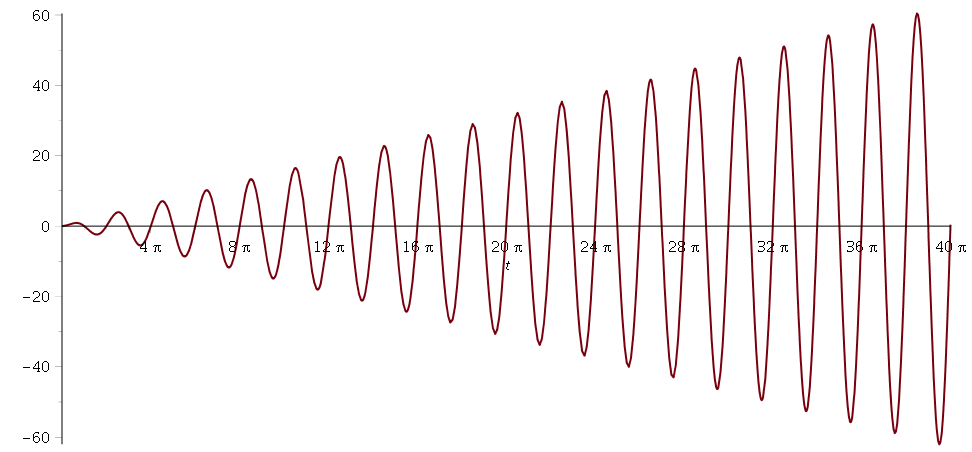
L'amplitude croit linéairement.

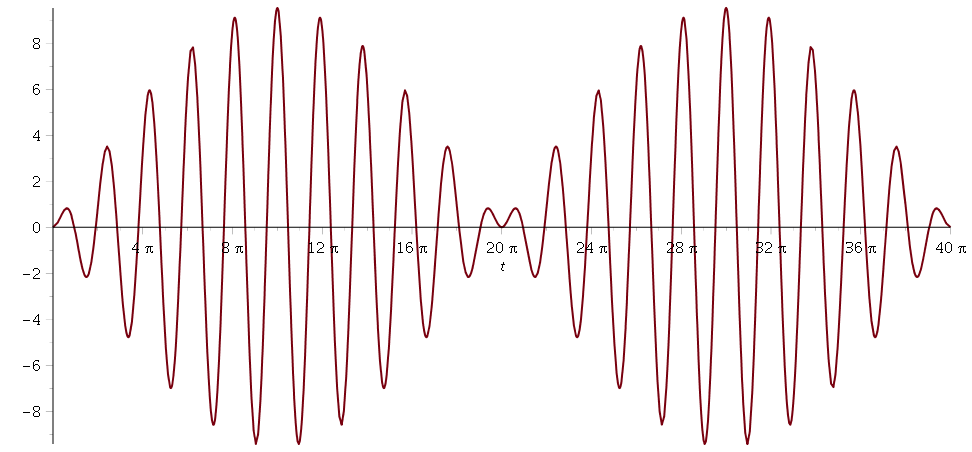
Voici deux illustrations représentant les variations de Y en fonction du temps (échelles arbitraires). La première correspond à \Omega=1,1\omega_{0} : on observe un phénomène de battement. La seconde correspond à \Omega=1,0001\omega_{0} : l'amplitude croît linéairement.
Bien sûr : tout cela est purement théorique puisqu'en réalité, il y a des frottements...

résonance avec un ressort

résonance avec un ressort

Posté par
cosmoffre : résonance avec un ressort 12-11-17 à 14:04

Merci beaucoup Vanoise pour l'explication détaillée, le résultat correspond à celui que je cherchais, bien qu'il ne soit pas réaliste je suis bien d'accord.

Une derniere petite chose. J'ai vu que l'on pouvait modéliser des liaisons moléculaires avec des ressorts. Donc si je marche sur un pont et que je saute sur celui ci à sa fréquence de résonance, alors le pont va osciller jusqu'à atteindre une amplitude max d'oscillation du aux frottements, d'ou l'interdiction aux soldats de marcher au pas sur un pont ?

Posté par
vanoisere : résonance avec un ressort 12-11-17 à 14:32

Bien vu !
Depuis 1850, les militaires ne doivent pas marcher au pas sur un pont ! D'autres accidents sont aussi arrivés avec des rafales de vents ayant approximativement pour fréquence, une fréquence propre du pont. Les architectes maritimes font aussi attention à ce que les fréquences propres des bateaux (roulis, tangage) soient éloignées des fréquences propres de passages des vagues, lorsque le bateau avance...
Plus de détails ici :

Posté par
cosmoffre : résonance avec un ressort 12-11-17 à 15:47

Ok parfait tout est clair !
Merci beaucoup de m'avoir donné de ton temps !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !