Bonsoir

Bonjour,
f=c/2l correspond à un tube ouvert, non ?

Pour la formule, j'ai en effet oublié un crochet à la fin, désolé.

Ztotale = Zr+Zm = j[(Mw-K/w)+(S*p*c)/tan(kl)]

Merci de votre réponse

Pourrais-tu poster un schéma du dispositif expérimental ?

Voila

Bonsoir
Ta présentation de l'expérience ne me paraît pas très réaliste : si tu fermes complètement le tuyau conformément à ton schéma, en supposant un dispositif de guidage imposant un mouvement vertical, l'ensemble (tube-air intérieur) va osciller un peu comme le ferait une masse accrochée à l'extrémité  d'un ressort dont l'autre extrémité  serait fixe, sans onde acoustique stationnaire dans le tube.
Ne vaut-il pas mieux imaginer un tuyau dont l'extrémité supérieure( sur le schéma) est fermée et dont l'autre extrémité est constitué d'un piston mobile pouvant osciller à la pulsation ? En pratique, ce piston mobile peut être la membrane d'un haut-parleure électro-dynamique (HP) alimenté sous courant sinusoïdal de pulsation .
La théorie du microphone électrodynamique est assez délicate et sans doute hors de sujet puisqu'elle fait intervenir des phénomènes d'induction et d'auto-induction. Une modélisation très simplifiée (voire simpliste) pourrait être la suivante.
On assimile la membrane à un piston d'aire S de masse M, soumise aux forces suivantes :
1° son poids compensé par l'action du bâti du HP : ces forces n'interviennent pas dans l'étude des oscillations ;
2° une force de rappel élastique : -K.x (x : élongation : primitive sinusoïdale de la vitesse)
3° une force dues au phénomène d'induction équivalente à une force de frottement fluide : - R.v (v : vitesse)
4° une force pressante exercée par l'air du tuyau : -p.S avec p : pression acoustique. l'étude des ondes acoustiques stationnaires (par exemple : corrigé question 4 du problème :"propagation dans un tuyau avec différentes terminaisons" ) conduit à une force d'expression (notations complexes) : j.c.S.v-/tan(k.l) avec k = 2/
5° une force motrice de Laplace de la forme : F_m.cos(.t)
En régime sinusoïdal et en utilisant les notations complexes, cela donne :




On peut définir une impédance du dispositif par :



En supposant l'amplitude de la force indépendante de la fréquence, (ce qui n'est pas tout à fait exact compte tenu de la largeur non infinie de la bande passante du micro...), l'amplitude de la vitesse de l'air à la sortie du tuyau sera inversement proportionnelle à l'inverse du module de l'impédance complexe. On peut donc s'intéresser aux variations en fonction de la pulsation de la grandeur :



Pour que les résultats dépendent moins des caractéristiques du HP, il est possible, à chaque fréquence de mesure, de régler l'alimentation du HP de façon qu'il fournisse une puissance acoustique fixe, cela bien sûr à condition de disposer d'un sonomètre précis dont la bande passante est connue. Dans ces conditions, l'impédance du HP seul peut être considérée comme constante :



Le terme sous la racine carrée s'écrit maintenant :



En supposant les fréquences d'étude supérieures à la fréquence propre du HP (moins d'une centaine de hertz en général) de façon à avoir : :





Y passe par des maximum successifs pour les valeurs de la pulsation qui rendent la tangente infinie soit pour des valeurs telles que :



Les maximums successifs correspondent aux fréquences propres du tuyau...
Sous toutes réserves évidemment : ce n'est peut-être pas ce que tu cherches à étudier...

Bonjour,
Le soucis c'est qu'ici, sauf erreur de ma part cela ne se comporte pas comme un HP.
En effet, la stimulation acoustique est transmise par la paroi de longueur l et se retrouve dans la cavité. Le piston a juste un rôle d'amortisseur.

Cordialement

Bonjour
C'est vrai que j'ai tenté une modélisation en essayant de modifier le moins possible ton schéma mais en "zappant" totalement le fait qu'il s'agit de modéliser un conduit auditif. J'espère tout de même que tu as bien compris que ton schéma est totalement irréaliste...
Une modélisation pourrait être la suivante :
le conduit est modélisé par un tuyau de longueur l dont l'extrémité supérieure est ouverte sur l'air extérieur de façon à être sensible aux ondes acoustiques se propageant dans l'air extérieur. Je suppose l'existence d'une telle onde sinusoïdale de fréquence f, de pulsation =2f.
L'extrémité inférieure est fermée par un piston mobile mais étanche de masse M, de surface d'aire S.
L'étude des forces appliquées à ce piston est analogue à cellee faite pour la membrane de HP, la force motrice en moins. Tu parles d'un piston amortisseur : il faut donc imaginer ce piston soumis à l'action d'un amortisseur exerçant sur le piston la force

Si tu applique la relation fondamentale de la dynamique au piston en régime sinusoïdal, on montre, (même méthode qu'au dessus) que, vis à vis d'une onde acoustique extérieure, le dispositif  possède une impédance :


C'est l'expression que tu obtiens avec en plus le terme R correspondant à l'amortissement. Comme précédemment, il peut être intéressant de l'intéresser aux variations en fonction de la fréquence de :


Si la pulsation propre de l'oscillateur :

est aussi une pulsation propre du tuyau :

on obtient une résonance aiguë car alors : Y = Y[sub]max[=1/R/sub]
Peut-être les choses sont-elles plus simples du point de vue numérique ; puisque (l/c) pour un conduit auditif est de l'ordre de 3.10^-5s, il est peut-être possible de considérer :

Voici un schéma correspondant à la modélisation d'au-dessus avec le piston en jaune, le ressort et l'amortisseur.

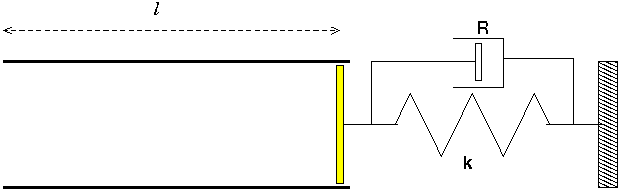
Merci de votre réponse, oui c'est en effet plus claire.
Je n'avais pas envisagé le fait que le tympan se comporte comme un piston. (Nous avons peu d'heures de physique, et jamais étudié les pistons..).

Par contre, je travail sur les résonances dans un conduit auditif fermé, l'onde accoustique provient de tissus cartilagineux du conduit auditif (transmises par la cordes vocales) et se retrouve bloqué dans l'espace entre le bouchon et le tympan.