Inscription / Connexion Nouveau Sujet
Resistances serie et parallèle
Bonsoir,
Alors voila je viens vers vous pour avoir une aide, un coup de pouce pour mon exercice de math.
Alors l'intitulé me dit que:
Deux résistors ont pour résistance respectives R1 et R2. Si les deux résistors sont montés en série, ils ont une résistance équivalente R = R1 + R2, et s'ils sont montés en parallèle, ils ont une résistance équivalente R' telle que: 1/R' = 1/R1 + 1/R2.
Peut on choisir R1 et R2 pour que R = 2,5 Ohm et R'= 0,4 Ohm ?
J'ai fait l'exercice et je souhaiterai juste me faire corriger et avoir le circuit (car le prof ma dit que se serai parfait de présenter l'exercice avec le circuit électronique)
Merci.
Réponse:
En série, on additionne les admittances.
1/R' = (1/r1) + (1/r2)
1/R' = (r2/r1.r2) + (r1/r1.r2)
1/R' = (r2 + r1)/(r1.r2)
R' = r1.r2/(r2 + r1) → on vous dit que : R' = 0,4 Ω
r1.r2/(r2 + r1) = 0,4
r1.r2 = (r2 + r1) * 0,4 → mais vous savez que : r1 + r2 = 2,5
r1.r2 = 2,5 * 0,4
r1.r2 = 1 ← résultat (2)
Vous recherchez deux réels (r1 et r2) dont vous connaissez la somme (S) et le produit (P).
…et bien ces 2 réels sont solutions de l'équation suivante :
x² - Sx + P = 0 → avec P, le produit, donc : r1.r2 = 1
x² - Sx + 1 = 0 → avec S, la somme, donc : r1 + r2 = 2,5
x² - 2,5x + 1 = 0
x² - 2,5x + (1,25² - 1,25²) + 1 = 0
x² - 2,5x + 1,25² - 1,25² + 1 = 0
(x² - 2,5x + 1,25²) - 1,25² + 1 = 0
(x² - 2,5x + 1,25²) - 0,5625 = 0
(x - 1,25)² - 0,5625 = 0
(x - 1,25)² = 0,5625
(x - 1,25)² = (± √0,75)²
x - 1,25 = ± 0,75
x = 1,25 ± 0,75
Premier cas : x = 1,25 + 0,75 → x = 2 Ω
Deuxième cas : x = 1,25 - 0,75 → x = 0,5 Ω
Les résistances sont donc : 2 Ω et 0,5 Ω
Maintenant il me manque juste le circuit...
Bonjour,
Ta méthode de calcul est très bonne: pour ma part je n'y pense jamais
De façon plus bestiale, une fois que tu avais établi que:
- r1 + r2 = 2,5
- r1 * r2 = 1
tu pouvais aussi écrire r2 = 2,5 - r1
et donc tu arrivais à r1 * (2,5 - r1) = 1
d'où l'équation du second degré à résoudre r12 - 2,5 * r1 + 1 = 0
L'autre façon de résoudre cette équation étant alors d'utiliser le discriminant  et les formules -b+/-
et les formules -b+/-
 /2a pour les racines lorsque
/2a pour les racines lorsque  >0
>0
Il ne manque pas un circuit mais 2 circuits car les mêmes résistances ne peuvent pas être montées en même temps en série et en parallèle (dans ce cas, ce serait 2 paires de résistances de valeur r1 et r2):
- le circuit où les 2 résistances sont montées en série,
- le circuit où les 2 résistances sont montées en parallèle.
Ces circuits sont ceux de la définition de ces types de montage que tu dois trouver dans ton cours justement pour t'introduire les formules que tu as utilisées pour trouver les valeurs r1 et r2
PS: Je ne comprends pas pourquoi on utilise le terme "résistor" qui est un anglicisme: vos professeurs ne respectent pas la loi qui donne la priorité à l'usage de notre langue, le Français? c'est en cours d'anglaus qu'on doit apprendre que résistance se traduit par resistor (sans accent!)
Tout d'abord je te remercie de m'avoir répondu.
Cependant, je n'ai aucun cours, c'est un exercice que j'ai choisis dans le polycopié que le prof nous à fournit.
Je bloque toujours pour les circuits...
PS: Je favorise l'utilisation de la langue française!!! Je lui dirai :p
Enfin si, c'est juste que j'ai pas assez cherché.
Voila les circuits (avec les mauvaises valeurs bien sure):
Circuit en série:
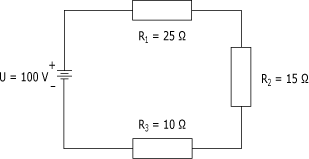
circuit en parallèle:
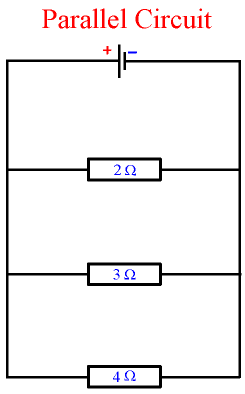
Voila l'autre méthode:
r1 et r2 en série
→ R = r1 + r2 = 2,5
r1 et r2 en //
→ 1/R' = (1/r1) + (1/r2)
→ 1/R' = [(1 * r2)/(r1 * r2)] + [(1 * r1)/(r1 * r2)]
→ 1/R' = [(1 * r2) + (1 * r1)]/(r1 * r2)
→ 1/R' = (r2 + r1)/(r1 * r2)
→ R' = (r1 * r2)/(r1 + r2) = 0,4
Vous avez donc : R qui est la somme
Vous avez dont : R' qui est le produit divisé par la somme
(a) : R = r1 + r2 = 2,5
(b) : R'= (r1 * r2)/(r1 + r2) = 0,4
→ r1 * r2 = 0,4(r1 + r2)
→ r1 * r2 = 0,4(2,5) = 1
Maintenant il suffit alors de résoudre l'équation X²-SX+P pour obtenir les valeurs cherchées:
Je trouve R' = 0,4 et R1 + R2 = 2,5
À partir de là je dois établir une équation du second degré:
X^2 - SX + P = 0
En remplaçant,
x^2 - (2,5)x + 1 = 0
Δ = 2,25
r1 = (- b - √Δ) / 2a = (2,5 - √2,25)/2 = 0,5 Ω
r2 = (- b - √Δ) / 2a = (2,5 + √2,25)/2 = 2 Ω


