Inscription / Connexion Nouveau Sujet
Résistance équivante
Bonjour,
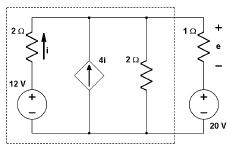
Considérant le circuit ci-dessous, je cherche à trouver l'équivalent de Thévenin de la portion encadrée.
J'ai réussi à trouver , mais je ne parviens pas à trouver
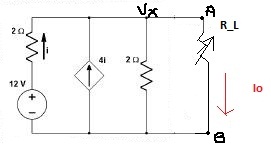
. J'ai voulu utiliser la méthode que l'on peut visualiser sur mon deuxième schéma, mais je ne parviens à rien... En fait, avec cette méthode, on cherche à exprimer
en identifiant pour trouver
.
Pouvez-vous m'aider svp ?
Merci d'avance.
PS : sur mon second schéma, a-t-on bien ?
Bonsoir
Pour trouver Rth, on déconnecte le circuit extérieur (le générateur de 20 V et la 1 ohm) (comme pour Eth). On éteint tous les générateurs et on remplace tous les générateurs par leur résistance interne. On calcule la résistance vue des bornes du générateur.
Là, on a donc 2 
en parallèle avec 2 donc 1
Si e est le Eth de la partie encadrée, ça ne peut pas être négatif.
Pour donner une valeur, il me faudrait la valeur du générateur de courant. 4 I ? A quoi est égal I ?
Je parle du e sur la droite du circuit, pas du Eth. Pour le courant, une loi des noeuds permet de trouver I=1A.
Si I = 1 A, le générateur de courant ayant une valeur de 4I (si j'arrive à bien lire sur le schéma) fait donc 4 A.
Dans ces conditions, je trouve e = 5 V.
Bon... Ça ne va du tout alors ! ^^
Selon toujours ce fameux "corrigé", on doit trouver Eth=10V, Rth=0,33 ohm et e=-7,5V. Je suis d'accord pour Eth. Le reste, je ne comprends pas.. Pouvez-vous m'indiquer votre méthode pour trouver e svp ?
on est censé déterminer e après avoir trouvé l'équivalent de Thévenin.
Oui, ça me paraît normal...
Pour e, j'ai trouvé Eth = 10 V et Rth = 1
comme décrit dans le message "Posté le 01-03-11 à 19:42".
Après, j'ai une maille avec Eth, Rth, la résistance de 1
et le générateur de 20 V.
On peut calculer I par exemple :
Ok, merci encore ! J'avais tenté dans cette même maille de trouver e avec une loi des mailles de cette façon :
10 - e - 20 - (tension aux bornes de Req) = 0, mais on se retrouve obligé de calculer le courant, du coup cela revient au même non ? Y aurait-il une autre méthode ? Simple curiosité.
Dernière chose, mon premier message, le "PS" 
Merci !
Oui, VA = VX puisque a et X sont reliés par un fil.
Avec la loi des mailles, on est obligé de calculer le courant à cause de la chute de tension dans Rth :
Eth - Rth i - e - 20 = 0
mais, pour calculer i, on est obligé de remplacer e par 1 x i parce qu'on ne connaît pas e (puisqu'on le cherche ! ).
On peut aussi utiliser Millman :
et :
Annuler
connectez vous