Bonjour,
1) Je trouverais plutôt R/3
2) Il faut redessiner le schéma sous une forme plus "classique" pour faire apparaître des triangles.
Il faut faire attention à la résistance R qui est commune aux deux triangles.
Avant d'appliquer la transformation triangle-étoile, il faut la remplacer par 2 résistances de 2R en parallèle, sinon on l'utilise 2 fois.
3) triangle-étoile également

Pour la 1, on arrive au schéma équivalent suivant :



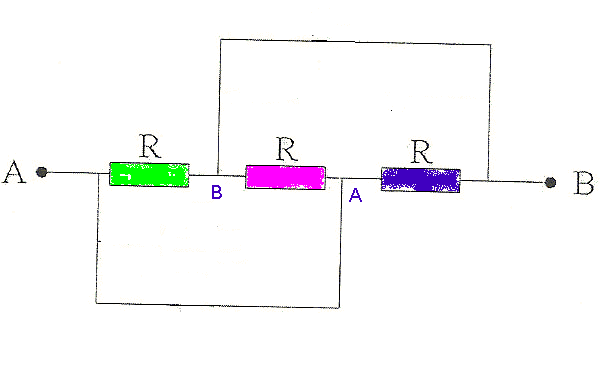
On voit que chacune des 3 résistances est connectée entre les points A et B

La résistance équivalente entre A et B est donc de 3 résistances R en parallèle -->

Req = R/3

2) Schéma équivalent avec les interrupteurs ouverts.



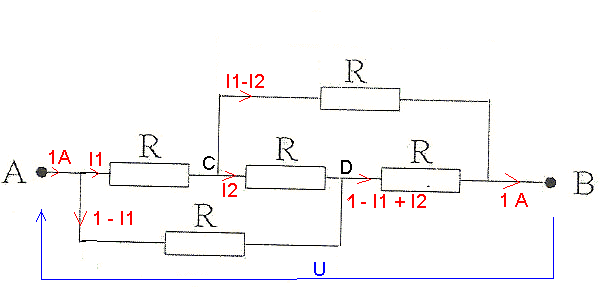
On injecte 1 A entre A et B et on calcule la différence de potentiel générée entre A et B.

R.I1 + R(I1 - I2) = U
R.I1 + R.I2 + R(1 - I1 + I2) = U
R(1-I1) + R(1-I1+I2) = U

R.(2I1 - I2) = U
R.(1 + 2I2) = U
R.(2-2I1+I2) = U

(2I1 - I2) = (1 + 2I2)
2.I1 = 1 + 3.I2

(1 + 2I2) = (2-2I1+I2)
I2 = 1 - 2I1

2.I1 = 1 + 3.(1 - 2I1)
8.I1 = 4

I1 = 1/2 A
I2 = 1 - 1 = 0 A

R.(1 + 2I2) = U
R.(1 + 0) = U

R(AB) = U/I (avec I injecté = 1A)

--> R(AB) = R
-----
Sauf distraction.  

Bonsoir,

Waouw J-P, c'est pas une méthode pour fainéant ça !

En redessinant le schéma avec les cinq résistances, on met vite en évidence un pont de Wheatstone... Il n'y a donc pas de courant dans la résistance du 'milieu' et on l'enlève illico du schéma. Reste la mise en // de deux résistances en série et la valeur équivalente est donc bien R.

Bonsoir,
La réponse de J-P est correcte mais fastidieuse.
En effet, il suffit d'appliquer le théorème de Kennely et transformer les 2 montages triangles en 2 montages étoiles. Dès lors, le montage se simplifie fortement et on obtient Rab = R.

Il faut employer ce qu'on a appris.
  
Si j'avais écrit (comme cela m'avait sauté au yeux) que, par raison de symétrie, la résistance entre C et D n'était parcourue par aucun courant dans le schéma du message du  12-10-09 à 13:32 et que donc elle pouvait être enlevée sans modifier la résistance équivalente entre A et B.
On avait alors directement R(AB) = 2R // 2R = R.
Cette méthode (celle que je viens de décrire) rejoint celle du message de ThierryMasula.

Mais je ne suis pas sûr qu'un débutant soit capable de le voir par lui-même ...

C'est  pourtant encore plus rapide et plus simple que de passer par le théorème de Kennely... qui peut-être n'est pas non plus connu par des débutants.
  
Plus il y a de méthodes données et plus il y des chances d'en avoir une à la portée de celui qui pose la question ...

3 méthodes pour le prix d'une, c'est donc très bien.

Bonjour tout le monde quelqu'un sait il calculer le résultat et pourquoi !
En vous remerciant

Bonsoir
Inutile ici d'appliquer la loi des nœuds et des mailles. En "tordant" un peu les fils et en les raccourcissant au besoin, il est facile de remarquer que, vu des bornes A et B, l'association est équivalente aux trois résistances branchées en parallèle.
Je te laisse conclure.

Merci pour ta réponse rapide,je t'avoue que j'ai du mal à comprendre .
J'applique la formule des résistances en parallèle je trouve 27.5

Les bornes reliées par un fil sont au même potentiel, soit celui de A  soit celui de B.
Dans le cas particulier où les 3 résistances sont égales, la résistance équivalente vaut (R /3)...

Et dans ce cas ! merci

Le montage est équivalent à une résistance de 11.  Pourquoi ajouter deux autres résistances  qui ne jouent aucun rôle puisqu'elles sont court-circuitées ?