Inscription / Connexion Nouveau Sujet
Réponse a un échelon de tension
Bonsoir. J'ai un problème avec les deux dernières questions de cet exercice. Est-ce que quelqu'un pourrait m'aider svp?
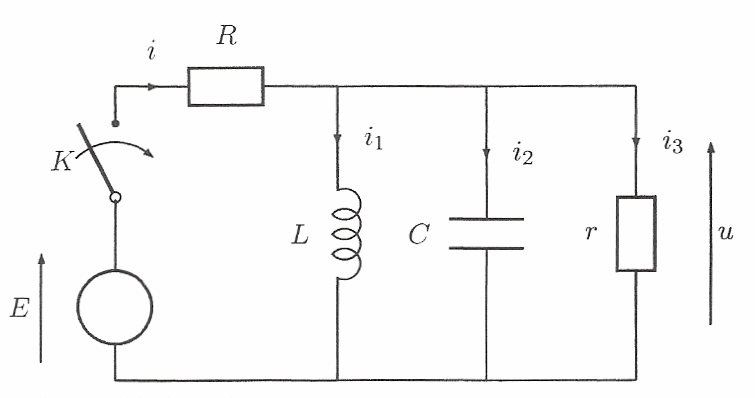
La figure ci- contre donne le schema du montage étudié. Le générateur de tension est idéal, de f.e.m. E constante. Les resistances constantes des deux conducteurs ohmiques sont notées R et r. Pour t<0, le condensateur, de capacité C, est déchargé et la bobine idéale, d'inductance L, n'est parcourue par aucun courant. A l'instant t=0, on ferme l'interrupteur. L'objet du problème est d'étudier l'évolution des grandeurs électriques dans le circuit pour t>0.
1. Determiner par un raisonnement simple, la tension u et les intensites i, i1, i2 et i3 dans les quatre branches:
- juste apres la fermeture de l'interrupteur (a t=0+);
- au bout d'une duree tres grande (quand t-> 
).
Pour t=0+: u(0+)=0; i(0+)= E/R; i1(0+)=0; i2(0+)E/R; i3(0+)=0
Pour t->: u(0+)=0; i(0+)= E/R; i1(0+)=0; i2(0+)E/R; i3(0+)=0
2. Etablir l'equation differentielle liant i3 a ses dérivées par rapport au temps t. On posera pour la suite:
0=1(
(LC)) et 
=(R+r)/(2RrC)
J'ai trouve: d2i3/dt + (r+R)/(RrC) di3/dt + 1/LC i3=0
2a. Quelle relation doit-il exister entre R,r,L et C pour que la solution de l'equation différentielle de la question précédente corresponde a un régime pseudo périodique?
Pour la suite, on prendra: R=2,50 k
, r=1,25 k, C=1,00 
F, L=20,0 mH
(2Rr)/(R+r)>(L/C)
2b. Calculer numeriquement la pulsation propore 0, la periode propre T0 ainsi que le coefficient . Que caractérise ?
0=7071 rad.s-1
T0=0,88 ms
= 600 rad.s-1
caractérise l'amortissement des oscillations.
2c. Definir et calculer la pseudo-pulsation et la pseudo-periode T.
=7045 rad.s-1
T=0,9 ms
2d. Determiner, en fonction du temps t, les expressions completes de la tension u et des intensites i, i1, i2 et i3 (on pourra utiliser et notamment pour alléger les expressions littérales). Calculer numériquement la valeur maximale de u si E=6,00 V (Je ne sais pas comment faire)
2e. Donner une estimation du temps nécessaire pour que le régime permanent soit pratiquement établi dans le circuit ( on admettra que c'est le cas a partir du moment ou l'amplitude de u devient inférieure au millième de sa valeur maximale). (Je n'ai également pas réussi a répondre a cette question)
Merci d'avance
1)
Pour t = 0+, c'est OK
erreurs pour t --> oo
u(oo) = 0 , i(oo) = E/R , i1(oo) = E/R , i2(oo) = 0 , i3(oo) = 0
-----
2)
u = r.i3
i2 = C.du/dt
u = L.di1/dt
i = i1 + i2 + i3
E - Ri = u
i2 = rC.di3/dt
r.i3 = L.di1/dt
i = i1 + i2 + i3
E - Ri = r.i3
r.i3 = L.di1/dt
i = i1 + rC.di3/dt + i3
E - Ri = r.i3
r.i3 = L.di1/dt
E - R(i1 + rC.di3/dt + i3) = r.i3
E - R(i1 + rC.di3/dt + i3) = r.i3, on dérive -->
- R(di1/dt + rC.di²3/dt² + di3/dt) = r.di3/dt
- R((r/L).i3 + rC.di²3/dt² + di3/dt) = r.di3/dt
- R(r.i3 + rCL.di²3/dt² + L.di3/dt) = rL.di3/dt
RrCL.d²i3/dt² + (r+R).L.di3/dt + Rr.i3 = 0
d²i3/dt² + [(r+R)/(RrC)].di3/dt + (1/(LC)).i3 = 0
--> ta réponse est OK.
Et avec ce qui est posé, on arrive à :
d²i3/dt² + Lambda.di3/dt + wo².i3 = 0
-----
2a)
Delta = Lambda² - 4wo²
Pseudo périodique si Delta < 0, donc si : Lambda² - 4wo² < 0
Lambda² < 4wo²
Lambda < 2wo
(R+r)/(2RrC) < 2/V(LC)
V(L/C) > 4.RrC/(R+r)
-----
2b)
L'unité de Lambda est le s^-1
-----
2c)
Je trouve pseudo pulsation = 7064 rad/s et pseudo période = 0,89 ms
-----
2d)
d²i3/dt² + Lambda.di3/dt + wo².i3 = 0
p² + Lambda.p + wo² = 0
p = [-Lambda +/- i.V(wo²-Lambda²)]/2
i3(t) = e^((-Lambda/2)t) * (A.cos(V(wo²-Lambda²).t) + B.sin(V(wo²-Lambda²).t)).
i3(0) = 0 ---> A = 0
i3(t) = B.e^((-Lambda/2).t) * sin(V(wo²-Lambda²).t)).
u = r.i3 -->
u(t) = r.B.e^((-Lambda/2).t) * sin(V(wo²-Lambda²).t)).
i2 = C.du/dt
i2 = C.r.B.[-(Lambda/2).e^((-Lambda/2).t).sin(V(wo²-Lambda²).t) + V(wo²-Lambda²).e^((-Lambda/2).t).cos(V(wo²-Lambda²).t]
i2(0) = E/R
E/R = C.r.B.[ V(wo²-Lambda²)]
B = E/[RrC.V(wo²-Lambda²)]
Et donc finalement:
i3(t) = E/[RrC.V(wo²-Lambda²)] * e^((-Lambda/2).t) * sin(V(wo²-Lambda²).t)).
u(t) = E/[RC.V(wo²-Lambda²)] * e^((-Lambda/2).t) * sin(V(wo²-Lambda²).t)).
i2 = C.du/dt
i2 = ...
E - Ri = u
i = (E - u)/R
i(t) = E/R - E/[R²C.V(wo²-Lambda²)] * e^((-Lambda/2).t) * sin(V(wo²-Lambda²).t)).
i = i1 + i2 + i3
i1 = i - i2 - i3 (et i, i2 et i3 ont été trouvé ci dessus, conc ...)
-----
Inutile de dire que je n'ai rien relu et que donc, il y a probablement des erreurs dans ce que j'ai écrit.
A toi de le trouver et de les corriger.
Bonne soiree et a bientot
Annuler
connectez vous