Niveau maths sup

Réponse à échelon de tension d'un circuit RLC.

Posté par
Linuks 11-11-09 à 14:34

Hello,

J'ai un peu soucis sur un exo de physique.
Je dois établir et résoudre l'équa diff vérifiée par i1(t).
Voici le shéma ainsi que mes premiers calculs.

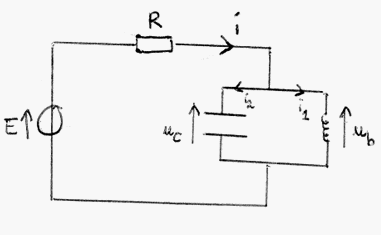
$Réponse à échelon de tension d\'un circuit RLC.$

** énoncé effacé ; image laissée **

Le condensateur est initialement déchargé.
Je trouves donc l'équation mais je bloque sur la 2ème condition initiale.
J'ai tout d'abord i1(0)=0 mais je ne vois pas quelle est l'autre condition...
Si quelqu'un pouvait m'aide ça serait sympa.
Merci

Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum

Posté par re : Réponse à échelon de tension d'un circuit RLC. 11-11-09 à 15:05

Voici donc l'énoncé :

R= 5000 ohms
C= 10^-6 farads
E= 10 volts
L= 25 henrys

1) Etablir l'équation différentielle verifiée par i1.
2) Résoudre cette équation.

Voici mes calculs avec l'équa diff que j'ai trouvé entourée en rouge : ** effacé **

Edit Coll : tu as tout ce qui est nécessaire pour écrire les résultats dans le forum

Posté par re : Réponse à échelon de tension d'un circuit RLC. 11-11-09 à 15:27

Okay, voilà donc l'équa diff

En applicant à la fois loi des noeuds et loi des mailles :

$i_1+i_2=i \\ u_c=u_b=u=L\times\frac{di_1}{dt} \\ i_2=+\frac{dq}{dt} \\ q=C\times u=C\times L\times\frac{di_1}{dt}$
Donc :
$i_2=+\frac{dq}{dt}=C\times L\times\frac{d^2i_1}{dt^2}$

En réarangeant le tout :

$\frac{d^2i_1}{dt^2}+\frac{1}{RC}\frac{di_1}{dt}+\frac{1}{LC}i_1=\frac{E}{RLC}$

Après avoir résolu l'équation caractéristique, j'ai :

$r_1=-100+100i\sqrt{3}$ et $r_2=-100-100i\sqrt{3}$

Et la je bloque sur les conditions initiales...
J'ai déjà :

$i_1(0)=0$

Mais il m'en faut une seconde pour résoudre l'équation différentielle homogène.

Posté par re : Réponse à échelon de tension d'un circuit RLC. 11-11-09 à 16:13

La tension aux bornes du condensateur est continue. Lorsque l'on applique la tension $E$ aux bornes du circuit à $t=0$ , la tension aux bornes du condensateur est nulle puisqu'il est initialement déchargé.

La tension initiale aux bornes de la bobine (qui s'exprime à partir de $i_1(t)$ ) doit donc être également nulle, non?

Posté par re : Réponse à échelon de tension d'un circuit RLC. 11-11-09 à 18:57

Oui c'est bien ça, on a donc ensuite la dérivée de $i_1$ en fonction du temps qui est nulle à t=0 car $u_c$ l'est aussi à cet instant.
Merci en tout cas :p

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Réponse à échelon de tension d'un circuit RLC.

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique