Bonsoir
L'intensité i traversant la charge ne dépend que de u et des caractéristiques de la charge. Si le générateur de tension u est idéal, autrement dit si la tension u est la même qu'elle que soit l'intensité fournie par le générateur, l'intensité i est la même en présence du condensateur. Bien sûr, loi des nœuds oblige, l'intensité du courant débité par le générateur n'est pas la même dans les deux cas : ii'.

Et dans un montage comme le suivant comment je peux savoir si est indépendente du courant ou non?

La situation est là nettement plus compliquée ! Ici la tension u_BA  ne sera pas la même si on branche entre A et B le dipôle d'impédance Z ou l'association {Z parallèle C'}. Mon raisonnement précédent ne s'applique pas.
Une méthode possible consiste à commencer par déterminer les caractéristiques du générateur de Thévenin équivalent au reste du circuit vue des bornes A et B (fém de Thévenin et impédance de Thévenin). On étudie ensuite le cas où ce générateur de Thévenin alimente Z puis le cas où ce générateur de Thévenin alimente {Z//C'} mais tout cela me parait un peu compliqué au niveau math sup. Pour une aide efficace, poste l'intégralité de l'énoncé.

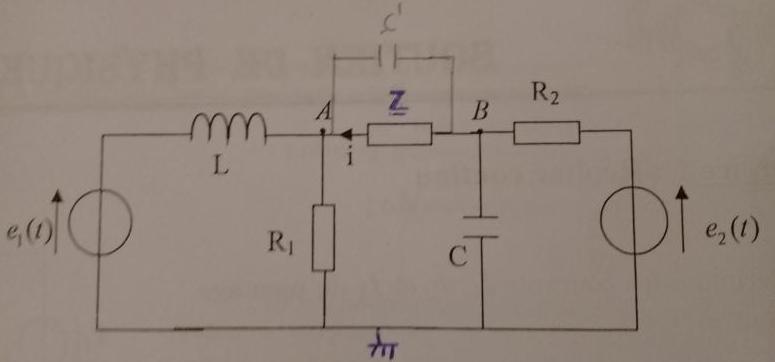
on considère le circuit de la figure ci dessous.
On donne:




I. 1. En appliquant le théorème de millman en A et B déterminer i(t) circulant dans le résistor R sous forme: . Calculer et .
2. Répondre à la question précédente en appliquant la transformation Thevenin-Norton.

II. On remplace le résistor R par un dipôle D d'inpédance complexe Z = .
1. Déterminer la valeur efficace complexe I du courant qui traverse le dipôle D. En déduire I.
2. Quelles valeurs de et pour que la puissance active consommée dans le dipôle D soit maximale.
(j'ai trouvé: et )
3. Déterminer dans ce cas, la puissance active consommée et le facteur de puissance du dipôle D.
(j'ai trouvé: et )
4. On désir augmenter le facteur de puissance, pour cela on branche un condensateur de capacité C' aux bornes du dipôle D. Calculer la valeur de C' pour que le nouveau facteur de puissance soit: (c'est là où je me bloque)

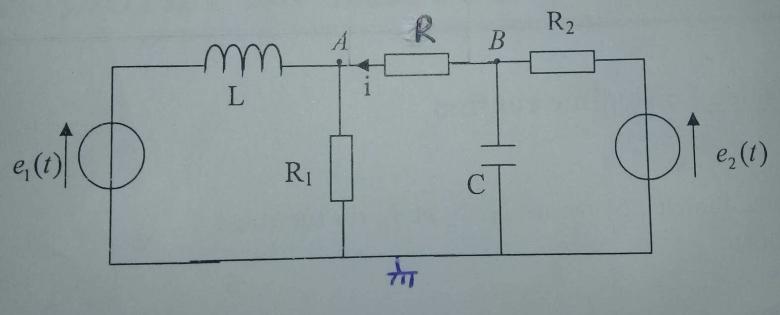
Ce problème n'est pas très facile mais tout de même moins compliqué que je ne craignais. Si je comprends bien, on te demande juste comment obtenir le nouveau facteur de puissance, pas de déterminer la nouvelle puissance active. Il suffit dans ces conditions d'écrire que l'argument 'de l'impédance complexe de l'association {Z//C'} vérifie :
cos(')=0,9

Je vais prendre un peu de temps ce soir pour vérifier ce que tu as fait déjà...

Merci Vanoise

La formule que tu  évoques est valide, comme tu l'écris pour une tension efficace  U imposée par le réseau et pour une puissance active fixée par les besoins de l'utilisateur. Cette formule ne s'applique pas ici comme déjà expliquée. Cet exercice est, me semble-t-il, conçu pour tester l'agilité des étudiants à étudier des circuits un peu compliqués en régime sinusoïdal. Je ne suis pas sûr que le circuit étudié ici ait un intérêt industriel.
Pour vérifier l'intérêt de l'ajout du condensateur, Il faudrait effectivement calculer la nouvelle puissance active, ce qui, comme expliqué, est possible mais un peu "calculatoire".

Je pense que dans la copie de l'énoncé, il faut lire 3R₂=100 et non 3R₃...
Sinon, pourrais-tu indiquer le résultat de ta transformation Thévenin- Norton ? Mes valeurs pour R₃ et X₃ sont différentes des tiennes...

oui vous avez raison pour le
pour j'ai trouvé:
A.N:
et
A.N:
voilà mon shéma:

je viens de refaire mon calcul et j'y ai trouvé une erreur, voilà mon résultat:

(en notation complexe)
d'où: (le module)
et (l'argument)
est ce que celles ci sont les bonnes valeurs?

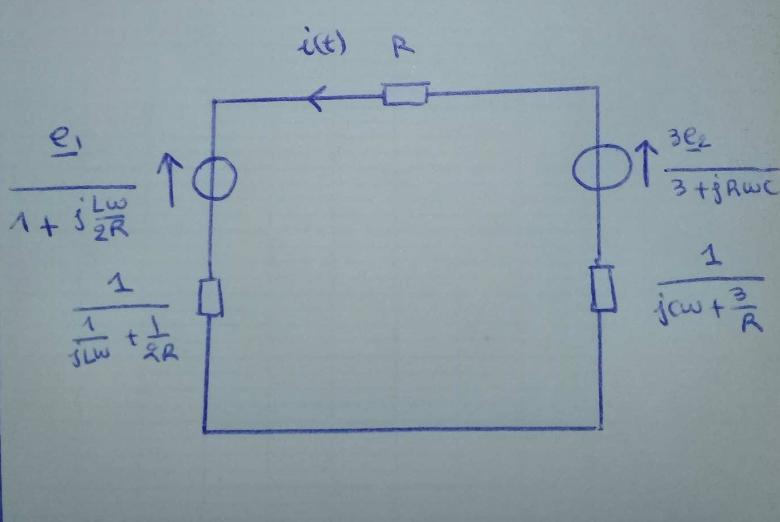
D'accord avec ton schéma équivalent. En regroupant les deux impédances, on obtient :



Les deux générateurs sont en opposition. Il sont équivalent à un générateur unique de fém :



puisque les valeurs instantanées des fém sont :


Les complexes associés valent :





On peut donc considérer le dipôle branché entre B et A comme alimenté par un générateur linéaire de tension unique de fém Eth et d'impédance interne Zth. La valeur complexe de l'intensité quand ce générateur alimente R vaut :


Je te laisse finir le calcul.
Pour la suite où on remplace R par un dipôle D d'impédance Z, on démontre que la puissance active consommée par D est maximale lorsque l'impédance de D est la valeur conjuguée de l'impédance du générateur de Thévenin qui l'alimente. Cela conduit à :



Je reconnais avoir fait tout cela un peu vite... Tu peux vérifier mes calculs et continuer.

Je vous remercie pour votre aide Vanoise

S'il vous plait est ce que je peux utiliser la formule pour obtenir les valeurs de et   sans que je sache si D est un dipôle passif linéaire ou non?

Oui. Cela devrait te conduire au résultat que je t'ai indiqué. Il est aussi possible de raisonner sur la puissance complexe mais cette grandeur n'est peut-être pas à ton programme.

Avec ZD = 70 - 70j (que je pense correct) ...

D a une impédance avec une composante capacitive ...
Tenter d'augmenter le facteur de puissance de D par un condensateur en // me semble bien hasardeux.

Sauf distraction.  

Comme déjà dit le but de cet exercice est d'entraîner les étudiants à l'étude de circuits en régime sinusoïdal. Pour l'intérêt pratique et industriel, cela sera fait j'espère dans d'autres exercices.

La remarque de JP est pertinente. Relever le facteur de puissance d'une installation où l'effet inductif est prépondérant (moteur par exemple) se fait en ajoutant en parallèle un condensateur. Inversement, relever le facteur de puissance d'un dipôle où l'effet capacitif est prépondérant (c'est le cas ici puisque  X₃<0) se fait en ajoutant en parallèle une bobine d'inductance L' dont on peut, pour simplifier, négliger la résistance interne. Dans l'énoncé, il faudrait donc remplacer C' par L'...

D'accord merci

Un peu d'aide pour t'aider à obtenir l'expression de la puissance active consommée par le dipôle D d'impédance complexe :


Le reste du circuit, comme cela a été démontré, est équivalent à un générateur linéaire de tension de fém E_th et d'impédance Z_th dont les expressions ont aussi été obtenues. Pour faire un raisonnement général littéral, je pose :




Le complexe associé à l'intensité traversant le dipôle D a pour expression :


Le carré de l'intensité maximale (amplitude de l'intensité) I_m vaut :




D'où l'expression de la puissance active consommée par le dipôle D :


En raisonnant sur la valeur efficace plutôt que sur l'amplitude de la fém, le facteur (1/2) disparaît... C'est peut-être comme cela que tu as l'habitude de faire...

Il faut donc, à E_m, R_th et X_th fixes, déterminer les valeurs de R₃ et X₃ qui rendent P_a maximale. Aucun calcul n'est nécessaire pour X₃ dans la mesure où cette valeur n'intervient qu'au dénominateur. Maximiser P_a revient à minimiser le dénominateur et la valeur minimale d'un carré est la valeur nulle. Il faut donc choisir :


Cela conduit à :



R₃ apparaît à la fois au numérateur et au dénominateur. Un calcul de dérivée et un tableau de variations que je te laisse faire, montrent que P_a est maximale pour :



Comme déjà dit, cela conduit à une impédance de D :




Avec tout cela, tu devrais bien avancer par toi-même...