Inscription / Connexion Nouveau Sujet
Relativité restreinte (addition relativiste des vitesses)
Bonjour,voilà j'ai un exercice en RR mais c'est une nouvelle matière et c'est vraiment très abstrait pour moi. Je vous le présente donc pour essayer d'obtenir un peu d'aide. Je complèterai le post au fur et à mesure qu'une idée me passe par la tête.
Je vous remercie d'avance.
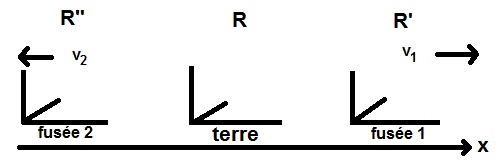
De la terre deux fusées sont envoyées en sens opposé, avec des vitesses respectives v1 et v2. cette situation pourrait inciter à conclure que pour des vitesses suffisamment proches de la vitesse de la lumière, un voyageur à bord de la première fusée verrait la deuxième s'échapper à une vitesse supérieure à celle de la lumière, ce qui serait incompatible avec la théorie de la relativité. Trouvez la faille dans ce raisonnement!
a) En supposant que la terre et les deux fusées représentent des référentiels galiléens, spécifiez des boosts de Lorentz, B' et B", liant les coordonnées terrestre d'un événement à celles de chacune des fusées.
b) Calculez la transformation de Lorentz entre les repères des deux fusées. Prouvez qu'il s'agit d'un boost en déterminant la vitesse v associée. Démontrez que cette vitesse reste inférieure à la vitesse de la lumière si les vitesses v1 et v2 le sont aussi. Déterminez la valeur de v pour v1 = v2 = 4c/5
c) Reformulez vos résultats en utilisant la rapidité rho = artanh(bêta). Démontrez l'additivité de cette grandeur. Les théorèmes d'addition des fonctions hyperboliques s'avèrent utiles.
Pour la question subsidiaire, du point de vue d'une des deux fusées, elles s'éloignent d'une certaine distance qui grandit à une vitesse supérieure à la vitesse de la lumière mais les vitesses respectives des 2 fusées restent inférieur à la vitesse de la lumière (je pense que c'est la faille dans ce raisonnement)
a) pour cette question il faut que je choisisse un événement mais je ne sais pas lequel (j'ai pensé à éventement décollage des deux fusées mais ce qui me semble l'événement le plus logique pour ce genre de question mais je n'en suis pas certain)
C'est surtout au niveau de la question "spécifiez des boosts de Lorentz B' et B" que je bloque car je ne sais pas comment faire.
J'aimerai d'abord commencer par résoudre cette question
Merci de votre aide
bonsoir,
"boost" est le terme anglais pour "transformation spéciale de Lorentz"
ici on te demande d'écrire donc les relations entre les événements (x,ct) dans R et (x',ct') dans R'
puis entre (x,ct) dans R et (x",ct") dans R"
bonsoir,
Si je choisi l'événement x (je ne sais pas à quoi il correspond du coup)
Je peux écrire:
(ct',x')=B'(ct,x) avec B' le premier Boost de Lorentz
(ct",x")=B"(ct,x) avec B" le second Boost de Lorentz
Mais comme les deux fusées partent en sens opposé (selon l'axe x) donc les boosts laissent invariant le sens de l'axe x.
pour R',  =v/c et pour R",
=v/c et pour R",  =-v/c
=-v/c
Je pense donc que B' = et B" =
avec g=

Est-ce correct?
oui mais attention, ici on a deux vitesses différentes v1 et v2 donc dans R' on a:  1,
1,  1 fct de v1
1 fct de v1
et dans R":  2,
2,  2 fct de v2
2 fct de v2
d'autre part pour le calcul j'écrirais plutôt:
(ct,x) = B' -1(ct',x')
(ct",x")=B"(ct,x) = B" B' -1(ct',x')
et de se ramener ainsi au calcul de B" B' -1
sauf erreur
Merci pour le lien J-P elle m'aide bien pour la 2eme question 
Par contre c'est pour la première question que je galère un peu..
On nous demande des Boosts de Lorentz (donc je dois trouver les matrices des boosts non?)
Si j'ai bien compris krinn, je dois avoir:
B' =
B" =
avec:
 1 = 1/
1 = 1/
 2 = 1/
2 = 1/
 1 =
1 =
 2 =
2 =
C'est bien ça? 
oui (en partant de ton post de 03:46)
on peut aussi éviter les signes - pour B" en posant b2 = v2/c
b) calculer B" B' -1 et prouver que c'est un "boost"
c) même chose en exprimant les matrices en fct de la rapidité
Ah ok je ne savais pas que pour prouver que c'est un boost il fallait calculer B"B'-1  (merci beaucoup)
(merci beaucoup)
Du coup j'ai B"B'-1 =
=
Est-ce correct? Je trouve que l'écriture est un peu lourde à cause des indices 1 et 2 du coup je ne vois pas comment cette matrice peut montrer que c'est un boost 
il faut lire mes posts en entier!
(ct',x')=B'(ct,x)
donc (ct,x) = B' -1(ct',x')
donc (ct",x")= B"(ct,x) donne (ct",x")= B" B' -1(ct',x')
B" B' -1 est donc bien la matrice de passage de R' à R"
si c'est un boost, cette matrice doit être de la forme:
 -
-

-


 et
et  étant fct de v (la vitesse cherchée) et n'étant pas indépendants
étant fct de v (la vitesse cherchée) et n'étant pas indépendants
on voit toute de suite par identification ce que pourrait valoir  , puis
, puis 
 (donc
(donc  )
)
mais il faut vérifier la relation liant  et
et  avant de pouvoir dire que ça correspond bien à une tranf. spéciale de Lorentz
avant de pouvoir dire que ça correspond bien à une tranf. spéciale de Lorentz
sauf erreur
Désolé je me suis un peu perdu..
Mais en regardant bien la matrice que B"B'-1 que j'ai calculée précédemment elle ne correspond donc pas à un boost car elle n'est pas de la forme
 -
-

-


et pourtant je l'ai calculé à partir des bonnes valeurs de B" et B'-1 (il me semble)
J'ai oublié de poster mais (ct",x")= B" B'-1(ct',x')

ct"=[ct'(1- 1
1 2)+x'(
2)+x'( 1-
1- 2)]
2)] 1
1 2
2
x"=[ct'( 1-
1- 2)+x'(1-
2)+x'(1- 1
1 2)]
2)] 1
1 2
2
je ne sais pas si c'est juste
Mais en regardant bien la matrice que B"B'-1 que j'ai calculée précédemment elle ne correspond donc pas à un boost
si, regarde mieux

si c'est un "boost" alors par identification on a forcément:
 =
=  1
1 2(1- B1 B2) (où B représente
2(1- B1 B2) (où B représente  )
)
et -B
 =
=  1
1 2(B1 -B2)
2(B1 -B2)
donc B = -(B1-B2)/(1-B1 B2) ce qui te donne la vitesse relative de R" / R' (B = v/c)
mais avant de dire cela il faut vérifier que B et
 sont bien reliée par la relation ...
sont bien reliée par la relation ...
sauf erreur



