Inscription / Connexion Nouveau Sujet
relation vectorielle
Bonjour,
J'ai une question bête sur les vecteurs ...
Nous avons la relation
Dans un aimant, on nous donne le sens de J donc H sera toujours opposé à J (si B est par exemple nul). Cependant H est négatif car il fournit de l'énergie au circuit électrique (avec un entrefer), H va t'il donc être dans le sens de J ?
Car ensuite on va dire que Ba = mu 0 Ha + Ja (sans vecteur), on suppose donc une projection ?
Merci
Bonjour
Il s'agit en effet d'une projection sur un axe qu'il faudrait définir ; les grandeurs qui interviennent étant ainsi des mesures algébriques dont les signes dépendent des sens des vecteurs.
Etant dans le cadran B>0, J>0 et H<0, et ne connaissant que J de l'aimant, peut on donc définir les autres vecteurs ? Afin de réaliser par exemple le théorème d'ampère ?
Je mets le schéma
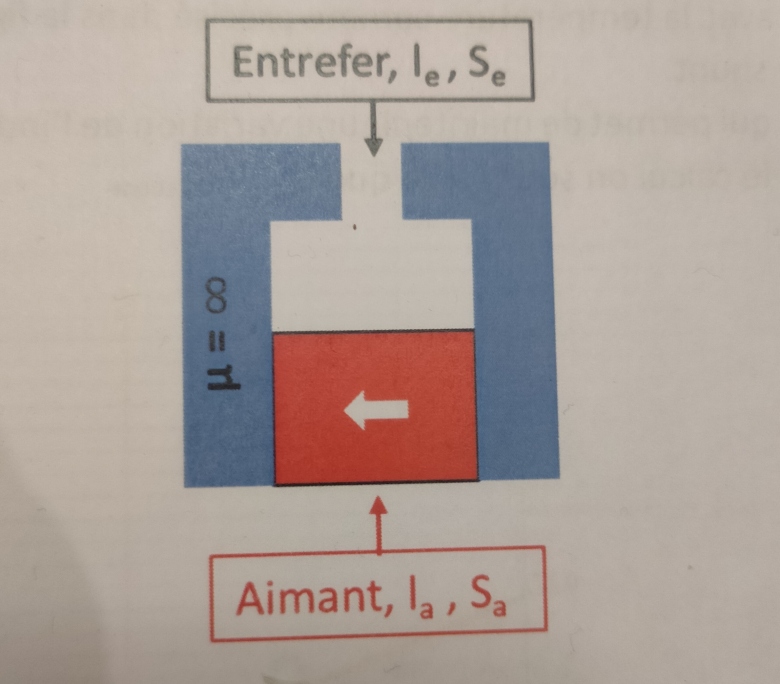
Merci !
Donc pas besoin des vecteurs pour le théorème d'ampère car celui ci "tourne" colinéairement au coutour avec I=0.
Je voudrais juste savoir si cela a du sens ce que je vais écrire :
Je peux écrire
On a la relation suivante :
Et Hx étant négatif est dans le sens contraire de Jx...
Oui ; cela résulte de la relation vectorielle générale que tu as écrite au début de ton premier message.


