Inscription / Connexion Nouveau Sujet
relation fréquence-tension d'un VCO
Bonsoir à tous,
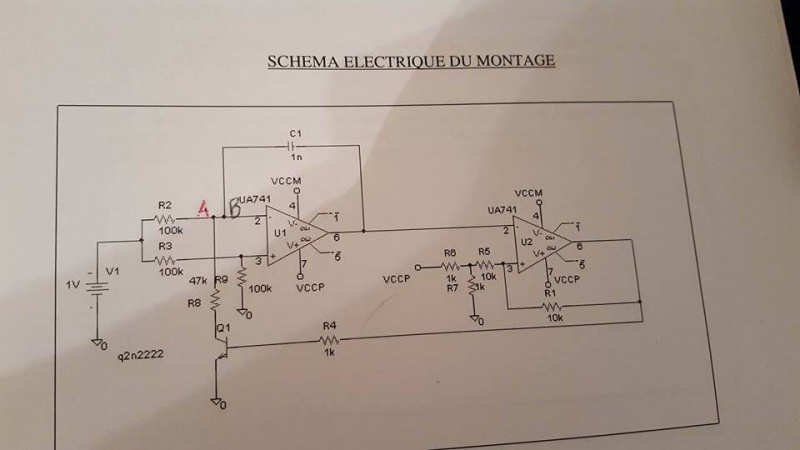
Alors voilà j'ai eu à réaliser un oscillateur commandé en tension dont le schéma du montage est sur l'image en pièce jointe. Il est constitué de deux étages à AOP, l'un en montage intégrateur l'autre en comparateur. J'ai pu, grâce à un logiciel tracer la caractéristique "Fréquence de sortie =f(tension d'entrée)" et il s'agit d'une droite passant quasiment par l'origine. Ainsi F=k*Ve
J'ai pu trouver expérimentalement que ce coefficient k vaut 2 V/s.
Maintenant il s'agit de corréler ce k avec la valeur théorique, or il faut dans un premier temps, l'expression et c'est là que je bute.
Pour débuter j'ai pris deux cas :
1) Le transistor Q1 est passant : En utilisant Milman sur le point A (ou B) on a
L'AOP 1 étant en mode linéaire
2) Le transistor Q1 est bloqué
L'AOP 1 étant en mode linéaire
Pour ce qui est de la suite je ne sais pas trop comment la gérer ^^ . Mon prof m'a dit qu'on pouvait passer soit par Milman soit par la loi des mailles, mais pour cette dernière je ne sais jamais quelle maille dégager pour mettre en équation.
Je me dis que si l'on passe comme ici par Milman et en considérant que diviser une tension par revient à la dériver, on pourrait obtenir une équation, mais je ne sais pas trop comment y arriver.
Je vous saurais gré de bien vouloir m'aider.
Cordialement.
Bonsoir,
Il te faut aussi étudier le comparateur...
Le théorème de Millman appliqué à E+ de U2 et au noeud entre R5 et R6 conduit à :
Tu en déduis les deux valeurs de la tension de sortie de U1 conduisant à des commutation de sortie de U2 :
Pour U1 : tu as réalisé l'étude en utilisant les complexes. C'est bien mais il faut maintenant en déduire les deux équations différentielles vérifiées par VS1 selon l'état de sortie de U2 en faisant intervenir V1 et les différentes résistances.
J'imagine que tu connais la méthode : une multiplication du complexe associé à une tension par (j )n correspond à la dérivée nième de la tension instantanée par rapport au temps. Tu vas arriver à une tension Vs1 correspondant à une exponentielle croissante puis une exponentielle décroissante selon l'état de Vs2. Des constantes de temps de ces deux branches d'exponentielles et des deux valeurs correspondant aux commutations, tu vas déterminer la période des tensions Vs1 et Vs2 ainsi que le rapport cyclique pour Vs2...
)n correspond à la dérivée nième de la tension instantanée par rapport au temps. Tu vas arriver à une tension Vs1 correspondant à une exponentielle croissante puis une exponentielle décroissante selon l'état de Vs2. Des constantes de temps de ces deux branches d'exponentielles et des deux valeurs correspondant aux commutations, tu vas déterminer la période des tensions Vs1 et Vs2 ainsi que le rapport cyclique pour Vs2...
Remarque : si tu n'as pas besoin d'une très grande précision, tu peux ici assimiler les branches d'exponentielles à des segments de droites...
Merci pour votre réponse mais pour ce n'est pas plutôt
en sachant que la résistance équivalente aux résistances R6, R5 et R7 vaut 21/11 ?
Honnêtement je n'arrive pas à ressortir les équations et je lorsque j'essaye avec la loi des mailles je n'y arrive pas non plus ><
En prenant l'égalité
On a
En divisant une tension par cela équivaut à la dériver, V1 étant constante, sa dérivée est nulle. On a alors :
Or cette dernière équation ne donne pas lieu à une exponentielle :/
P.S : le V1/2 vient du fait que R9 et R3 ont même valeur.
Je rectifie mes deux dernières équations :
On a
En divisant une tension par Z_{C1} cela équivaut à la dériver, V1 étant constante, sa dérivée est nulle. On a alors :
Or cette dernière équation ne donne pas lieu à une exponentielle :/
Tu fais bien de m'interroger sur mes calculs : il m'arrive de commettre des étourderies. Voici le détail pour les valeurs de commutations de VS1 :
Je note V5 le potentiel du nœud commun à R5 et R6 et R7 :
Théorème de Millman appliqué en E+ :
Par substitution de façon à éliminer V5 :
Les applications numériques sont d'ailleurs conformes au maximum et au minimum de V_{S1} obtenus en simulant le circuit sous PSPICE.
Ah au temps pour moi, merci pour ta réponse.
Que penses-tu de l'équation que j'ai écrite dans les messages suivants ? Pourquoi est-ce que je ne retrouve pas l'exponentielle ?
À propos des équations différentielles vérifiées par VS1 :
Si Q1 est bloqué, j'obtiens le même résultat que toi :
Si Q1 est passant, j'obtiens :
Puisque R2 > R8, cela donne deux segments de droite, l'un de coefficient directeur positif, l'autre de coefficient directeur négatif conformément à la simulation.
Tu n'a plus qu'à déterminer la période et le rapport cyclique.
Remarque : Tu as sans doute vu en cours qu'un tel montage ne fonctionne pas avec des ampli op réels :pour obtenir un fonctionnement satisfaisant, il faut placer en parallèle avec C un conducteur de résistance très supérieure à l'impédance de C : 1M par exemple. Dans ce cas, on obtient théoriquement des branches d'exponentielles mais, à cause de la grande valeur de la résistance, elles sont pratiquement assimilables à des segments de droite. J'aurais dû être plus précis sur ce point dans mon message précédent.
par exemple. Dans ce cas, on obtient théoriquement des branches d'exponentielles mais, à cause de la grande valeur de la résistance, elles sont pratiquement assimilables à des segments de droite. J'aurais dû être plus précis sur ce point dans mon message précédent.
Merci beaucoup 
Une dernière question : comment se fait-il que l'on ait VS1 à la place de V1 dans ces équations ?
Désolé : grosse étourderie de ma part : il s'agit de V1 bien sûr :
Toutes mes excuses mais il se fait tard...
Revérifie tes signes : en fait je n'obtiens pas exactement ton résultat pour Q1 bloqué...
En divisant une tension par Z_{C1} cela équivaut à la dériver,
De façon générale, c'est
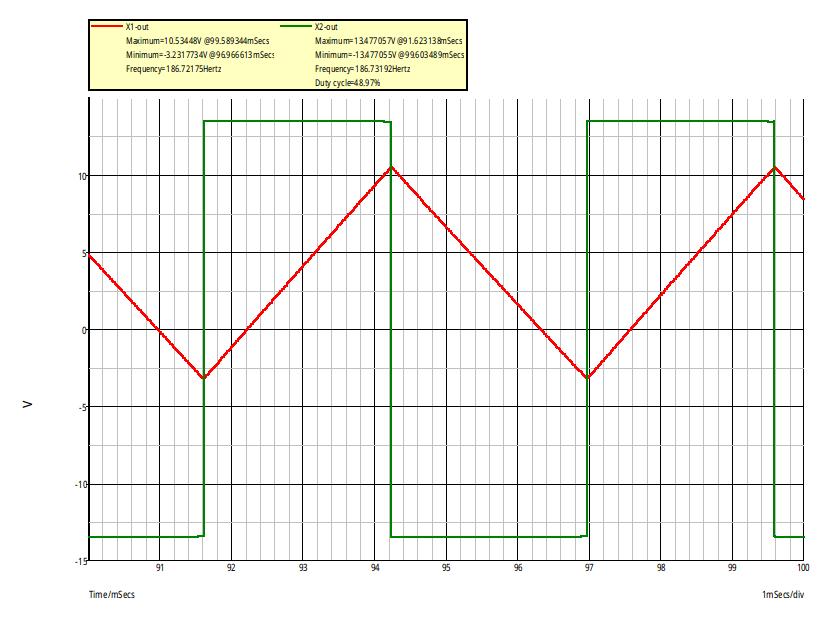
Voici la simulation que j'ai obtenue avec Vcc=15V. Les autres valeurs apparaissent au dessus des courbes.
Super j'ai tout compris.
Effectivement je devais sûrement avoir une erreur de signe, étourdi que je suis.
Diviser par revient à multiplier par
et la présence du
implique la dérivation, si je ne me trompe ?
Mais effectivement, de manière générale je ne suis pas une lumière en électronique ^^.
Je vous remercie d'avoir consacré une partie de votre soirée à me répondre  ( surtout que demain c'est début de semaine )
( surtout que demain c'est début de semaine )
Diviser par
oui mais cette dérivée est aussi multipliée par C1, ce que ne laissait pas entendre ta phrase précédente :
En divisant une tension par
Bonsoir, je relance le sujet juste pour poser une dernière question : ais-je juste lorsque je dis qu'une tension continue divisée par donne 0 par rapport au temps ? Ou bien avez-vous suivi un autre raisonnement pour avoir un second membre nul dans vos équations ?
En vous remerciant.
Bonsoir
Ta méthode est sans doute bonne mais mal exprimée. De façon générale, quand tu as comme ici un circuit un peu compliqué, tu peux procéder en trois étapes :
1° étudier le circuit en utilisant les complexes comme si le régime était sinusoïdal permanent ;
2° en déduire les équations différentielles vérifiées en régime sinusoïdal sachant que multiplier un complexe par (j )n est équivalent à en prendre la dérivée nième par rapport au temps ;
)n est équivalent à en prendre la dérivée nième par rapport au temps ;
3° admettre que les équations différentielles ainsi démontrées en régime sinusoïdal sont aussi valides en régime quelconque.
Remarque : dériver correspond à multiplier par j ; ce n'est pas la même chose que diviser par Zc : la capacité du condensateur est en trop !
; ce n'est pas la même chose que diviser par Zc : la capacité du condensateur est en trop !


