Bonjour
Il faut commencer par démontrer que, dans les conditions de Gauss, le foyer est le milieu du segment SC (S : sommet, C : centre). Il faut ensuite tracer les rayons particuliers qui permettent d'obtenir l'image A'B' d'un objet AB.
On exprime ensuite de façons différentes le grandissement transversal. On obtient les relations de conjugaison en identifiant les différentes expressions  obtenues du grandissement.
Plus de détail ici, en particulier pages XIII-5 et suivantes :

Bonjour merci pour la réponse !

J'ai compris presque tout, mais comment on montre que le foyer image est au milieu de SC parce que sur ça je bloque ?

C'est vrai que l'explication fournie sur le document que je t'ai recommandé est un peu succincte.
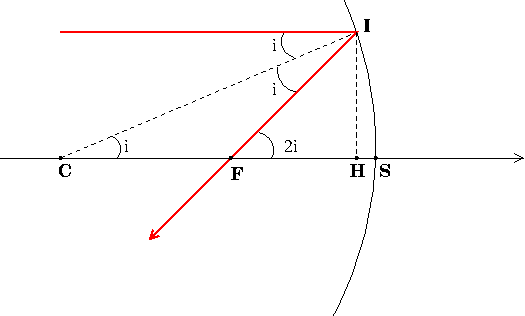
Voici un schéma qui devrait t'aider. Un rayon incident parallèle à l'axe optique se réfléchit en passant par F.
La loi de Descartes sur la réflexion et les propriétés des angles alternes internes conduisent au relations simples entre les angles indiquées sur mon schéma.
Je te rappelle que, dans les conditions de Gauss, le point I est toujours très proche de l'axe optique ; les angles sont tous très petits de sorte que :
sin(i)tan(i)i (en radians)
cos(i)1
Dans ces conditions, il est facile de montrer que F est le milieu du segment (CH) et que H est quasiment confondu avec S...