Bonjour à tous,
Je rencontre quelques difficultés pour un DM de Physique de PSI, sur les systèmes linéaires. Voici l'énoncé (Issu du Concours X-ENS 1997 (disponible ici : ) :
"On s'intéresse dans cette partie à la régulation de l'intensité B d'un champ magnétique. On dispose d'une grandeur ramenée U_r proportionnelle à B (U_r = k.B) où k est supposée invariable quelles que soient les conditions de fonctionnement. L'utilisateur peut choisir une tension de consigne U_c et on désire obtenir une loi de commande B = f(U_c) linéaire de pente m= 0,22 T/V avec une tolérance sur cette valeur de 1%.
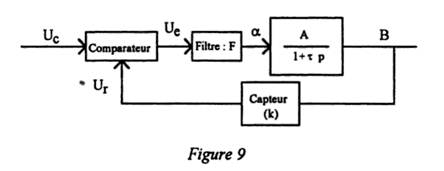
La structure de la boucle d'asservissement est proposée figure 9 : F est un système linéaire de grandeur d'entrée U_e=U_c-U_r et de grandeur de sortie .
On admettra dans la suite que la relation entre et B est linéaire de fonction de transfert A/(1+p) où le coefficient A, du fait de variations des conditions de fonctionnement du dispositif, peut prendre sa valeur dans l'intervalle [A₀-A,A₀+A] avec A₀ = 1,37 T/V et A = 0,1 T/V. En outre, = 1,32 ms.

On désire déterminer la structure du filtre F et la valeur qu'il convient de donner à k.
1)SOLUTION PROPORTIONNELLE.
Le filtre F le plus simple envisageable est un opérateur "multiplication de gain K" : =KU (valeur limitée à _max = 0,9 par une saturation).
a) Déterminer alors les valeurs de k et K qui conviennent en régime permanent.
b) Si l'on en modifie instantanément la consigne de 4 à 4,5 volts (A valant A₀ = 1,37 T/V), décrire le comportement du système et tracer l'évolution de B au cours du temps.


Pour la question a), j'ai du mal à saisir les conséquences de l'information "régime permanent" : Cela signifie que U_r=U_c ? Dans ce cas, comment calculer k et K, vu que =KU=K(U_c-U_r ??

Pour la question b), Il faut faire une fonction transfert de U_c et B, c'est bien cela ?


Je vous remercie pour le temps que vous consacrerez à mon problème.